 por Guilhermeds » Qua Mai 30, 2012 16:40
por Guilhermeds » Qua Mai 30, 2012 16:40
Boa Tarde,
Então estou com dificuldades para encontrar o ponto crítico dessa função:
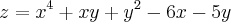
Se alguém puder me ajudar fico agradecido.
att,
Guilherme.
-
Guilhermeds
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Mai 30, 2012 16:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: eng eletrônica
- Andamento: cursando
 por Molina » Qua Mai 30, 2012 17:14
por Molina » Qua Mai 30, 2012 17:14
Boa tarde,
Guilherme.
Você terá que fazer o uso de derivadas parciais de x e de y, igualando-as a 0. Assim:

e
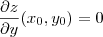
Você já viu este conteúdo?
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Guilhermeds » Qua Mai 30, 2012 17:39
por Guilhermeds » Qua Mai 30, 2012 17:39
Obrigado por responder Molina.
Mais então, eu fiz o uso das derivadas em relação a x e y.

e

correto né ?
E chegou num sistema que não consigo resolver que seria :
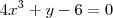
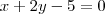
-
Guilhermeds
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Mai 30, 2012 16:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: eng eletrônica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [ponto critico]duvida sobre achar o ponto critico
por nayra suelen » Dom Mai 27, 2012 19:38
- 2 Respostas
- 2436 Exibições
- Última mensagem por nayra suelen

Qua Mai 30, 2012 13:23
Cálculo: Limites, Derivadas e Integrais
-
- [Ponto Crítico e Ponto de Inflexão e intervalos] Dúvidas em
por Andre Lopes » Qua Set 26, 2012 00:37
- 2 Respostas
- 3375 Exibições
- Última mensagem por MarceloFantini

Qui Set 27, 2012 06:56
Cálculo: Limites, Derivadas e Integrais
-
- derivadas ponto critico
 por eulercx » Ter Jan 26, 2016 11:54
por eulercx » Ter Jan 26, 2016 11:54
- 2 Respostas
- 2296 Exibições
- Última mensagem por adauto martins

Qui Jan 28, 2016 10:09
Cálculo: Limites, Derivadas e Integrais
-
- Ponto Crítico / Intervalos Cres. Decres. / Min. e Máx.
por Fabio Cabral » Sex Jun 17, 2011 12:23
- 5 Respostas
- 3081 Exibições
- Última mensagem por LuizAquino

Dom Jun 19, 2011 16:25
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Derivadas parciais e ponto crítico
por Mell » Dom Jul 07, 2013 10:24
- 1 Respostas
- 1916 Exibições
- Última mensagem por hygorvv

Seg Jul 08, 2013 07:11
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 12 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
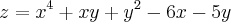

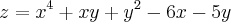


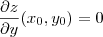



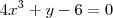
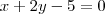

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.