Calcule a integral iterada
 e esboce sua região de integração R.
e esboce sua região de integração R.Se alguém puder me ajudar, ficarei grato.
Aguardo retorno.

 e esboce sua região de integração R.
e esboce sua região de integração R.
Cleyson007 escreveu:Bom dia a todos!
Calcule a integral iteradae esboce sua região de integração R.

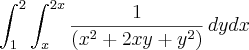


Cleyson007 escreveu:Apresentando minha resolução:
Primeiramente, gostaria de saber se até aqui está correto.
![\int_x^{2x} \frac{1}{(x+y)^2}\, dy = \int_{2x}^{3x} \frac{1}{u^2}\, du = \left[-\frac{1}{u}\right]_{2x}^{3x} = -\frac{1}{3x} + \frac{1}{2x} \int_x^{2x} \frac{1}{(x+y)^2}\, dy = \int_{2x}^{3x} \frac{1}{u^2}\, du = \left[-\frac{1}{u}\right]_{2x}^{3x} = -\frac{1}{3x} + \frac{1}{2x}](/latexrender/pictures/8e7922710d06bd7ad7ce91cdad4b84cf.png)


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.