 por engrangel » Qua Abr 18, 2012 15:46
por engrangel » Qua Abr 18, 2012 15:46
gostaria de saber se alguem pode me informar uma previa de qual o primeiro passo para se resolver questoes envolvendo integrais por frações parciais. Pois estou dando inicio a esse assunto , mas nao consigo acompanha-lo. segue uma questão e gostaria se alguem soubesse responder , postasse o passo a passo da questao para um melhor entendimento.
questao:
- Anexos
-
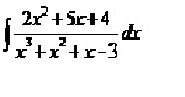
- Sem título.jpg (6.04 KiB) Exibido 2934 vezes
-
engrangel
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Abr 18, 2012 15:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia civil
- Andamento: cursando
 por LuizAquino » Qui Abr 19, 2012 14:53
por LuizAquino » Qui Abr 19, 2012 14:53
engrangel escreveu:gostaria de saber se alguem pode me informar uma previa de qual o primeiro passo para se resolver questoes envolvendo integrais por frações parciais. Pois estou dando inicio a esse assunto , mas nao consigo acompanha-lo. segue uma questão e gostaria se alguem soubesse responder , postasse o passo a passo da questao para um melhor entendimento.
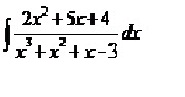
- figura1.jpg (6.04 KiB) Exibido 2924 vezes
Se você deseja estudar esse conteúdo, então eu gostaria de recomendar as videoaulas "29. Cálculo I - Integração por Frações Parciais (Caso I e II)" e "30. Cálculo I - Integração por Frações Parciais (Caso III e IV)". Elas videoaulas estão disponíveis em meu canal no YouTube:
http://www.youtube.com/LCMAquinoAlém disso, para estudar a resolução dessa integral você pode usar um programa. Por exemplo, o
SAGE, o Mathematica, o Maple, etc.
Alguns desses programas são disponibilizados também na forma de uma página na internet. É o caso do
SAGE Notebook e do Mathematica. Por exemplo, siga os passos abaixo para conferir a resolução.
- Acesse a página: http://www.wolframalpha.com/
- No campo de entrada, digite:
- Código: Selecionar todos
integrate (2x^2 + 5x + 4)/(x^3 + x^2 + x - 3) dx
- Clique no botão de igual ao lado do campo de entrada.
- Espere aparecer o resultado da derivada. Clique então no botão "Show steps" que fica ao lado do resultado.
- Pronto! Agora basta estudar o procedimento.
Por fim, para que você possa digitar as notações adequadas aqui no fórum, eu aproveito para indicar o seguinte tópico:
DICA: Escrevendo Fórmulas com LaTeX via BBCodeviewtopic.php?f=9&t=74
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por engrangel » Qui Abr 19, 2012 17:47
por engrangel » Qui Abr 19, 2012 17:47
cara
obrigado pela dica e pelas informações, me ajudou muito.
-
engrangel
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Abr 18, 2012 15:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia civil
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Frações parciais.
por 380625 » Sex Jul 05, 2013 15:18
- 5 Respostas
- 3145 Exibições
- Última mensagem por young_jedi

Sáb Jul 13, 2013 10:41
Álgebra Elementar
-
- frações parciais
por fasaatyro » Qui Dez 04, 2014 09:18
- 1 Respostas
- 1149 Exibições
- Última mensagem por lucas_carvalho

Qui Dez 04, 2014 11:28
Cálculo: Limites, Derivadas e Integrais
-
- Integral por Frações Parciais
por Bruhh » Qua Set 29, 2010 18:20
- 2 Respostas
- 5399 Exibições
- Última mensagem por Bruhh

Qui Set 30, 2010 08:40
Cálculo: Limites, Derivadas e Integrais
-
- [integral] fraçoes parciais
por ewald » Qui Set 08, 2011 15:10
- 1 Respostas
- 2112 Exibições
- Última mensagem por Neperiano

Qui Set 08, 2011 15:47
Cálculo: Limites, Derivadas e Integrais
-
- integral frações parciais
por paolaads » Seg Out 22, 2012 21:08
- 3 Respostas
- 2471 Exibições
- Última mensagem por MarceloFantini

Ter Out 23, 2012 18:56
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





 , avisa que eu resolvo.
, avisa que eu resolvo.

