Calcule a integral iterada
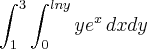 e esboce a região de integração R, sobre a qual a integral é calculada.
e esboce a região de integração R, sobre a qual a integral é calculada.Aguardo retorno.

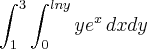 e esboce a região de integração R, sobre a qual a integral é calculada.
e esboce a região de integração R, sobre a qual a integral é calculada.
Cleyson007 escreveu:Calcule a integral iteradae esboce a região de integração R, sobre a qual a integral é calculada.
 restrito ao intervalo [ln 1, ln 3]);
restrito ao intervalo [ln 1, ln 3]);
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes