por engrangel » Qua Abr 18, 2012 15:46
gostaria de saber se alguem pode me informar uma previa de qual o primeiro passo para se resolver questoes envolvendo integrais por frações parciais. Pois estou dando inicio a esse assunto , mas nao consigo acompanha-lo. segue uma questão e gostaria se alguem soubesse responder , postasse o passo a passo da questao para um melhor entendimento.
questao:
- Anexos
-
- Sem título.jpg (6.04 KiB) Exibido 2856 vezes
-
engrangel
- Novo Usuário
-
- Mensagens: 2
- Registrado em: Qua Abr 18, 2012 15:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia civil
- Andamento: cursando
por LuizAquino » Qui Abr 19, 2012 14:53
engrangel escreveu:gostaria de saber se alguem pode me informar uma previa de qual o primeiro passo para se resolver questoes envolvendo integrais por frações parciais. Pois estou dando inicio a esse assunto , mas nao consigo acompanha-lo. segue uma questão e gostaria se alguem soubesse responder , postasse o passo a passo da questao para um melhor entendimento.
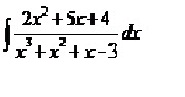
- figura1.jpg (6.04 KiB) Exibido 2846 vezes
Se você deseja estudar esse conteúdo, então eu gostaria de recomendar as videoaulas "29. Cálculo I - Integração por Frações Parciais (Caso I e II)" e "30. Cálculo I - Integração por Frações Parciais (Caso III e IV)". Elas videoaulas estão disponíveis em meu canal no YouTube:
http://www.youtube.com/LCMAquinoAlém disso, para estudar a resolução dessa integral você pode usar um programa. Por exemplo, o
SAGE, o Mathematica, o Maple, etc.
Alguns desses programas são disponibilizados também na forma de uma página na internet. É o caso do
SAGE Notebook e do Mathematica. Por exemplo, siga os passos abaixo para conferir a resolução.
- Acesse a página: http://www.wolframalpha.com/
- No campo de entrada, digite:
- Código: Selecionar todos
integrate (2x^2 + 5x + 4)/(x^3 + x^2 + x - 3) dx
- Clique no botão de igual ao lado do campo de entrada.
- Espere aparecer o resultado da derivada. Clique então no botão "Show steps" que fica ao lado do resultado.
- Pronto! Agora basta estudar o procedimento.
Por fim, para que você possa digitar as notações adequadas aqui no fórum, eu aproveito para indicar o seguinte tópico:
DICA: Escrevendo Fórmulas com LaTeX via BBCodeviewtopic.php?f=9&t=74
-
LuizAquino
- Colaborador Moderador - Professor
-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
por engrangel » Qui Abr 19, 2012 17:47
cara
obrigado pela dica e pelas informações, me ajudou muito.
-
engrangel
- Novo Usuário
-
- Mensagens: 2
- Registrado em: Qua Abr 18, 2012 15:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia civil
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Frações parciais.
por 380625 » Sex Jul 05, 2013 15:18
- 5 Respostas
- 3028 Exibições
- Última mensagem por young_jedi
Sáb Jul 13, 2013 10:41
Álgebra Elementar
-
- frações parciais
por fasaatyro » Qui Dez 04, 2014 09:18
- 1 Respostas
- 1104 Exibições
- Última mensagem por lucas_carvalho
Qui Dez 04, 2014 11:28
Cálculo: Limites, Derivadas e Integrais
-
- Integral por Frações Parciais
por Bruhh » Qua Set 29, 2010 18:20
- 2 Respostas
- 5297 Exibições
- Última mensagem por Bruhh
Qui Set 30, 2010 08:40
Cálculo: Limites, Derivadas e Integrais
-
- [integral] fraçoes parciais
por ewald » Qui Set 08, 2011 15:10
- 1 Respostas
- 2021 Exibições
- Última mensagem por Neperiano
Qui Set 08, 2011 15:47
Cálculo: Limites, Derivadas e Integrais
-
- integral frações parciais
por paolaads » Seg Out 22, 2012 21:08
- 3 Respostas
- 2322 Exibições
- Última mensagem por MarceloFantini
Ter Out 23, 2012 18:56
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de
Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é
Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:
Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:
Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
