 por ricardosanto » Ter Abr 17, 2012 22:34
por ricardosanto » Ter Abr 17, 2012 22:34
busquei a ajuda desse fórum, pelo motivo de o meu pro ñ ajudar na resolução de questões.
foi no meu ultimo post q o LuizAquino(obrigado meu irmão) me mandou um site q está me ajudando muito, mas mesmo assim, ele não resolveu completamente o meu problema. que é quando se aplica todas as regras de derivação daí devemos simplificar.

tipo a resolução assimaeu consigo entender até em E^x x³ e^x(3x²)
como que ele transforma isto em e^x x²(x+3)?
desde já obrigado.
-
ricardosanto
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Seg Abr 16, 2012 12:17
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia civil
- Andamento: cursando
 por TheoFerraz » Ter Abr 17, 2012 23:42
por TheoFerraz » Ter Abr 17, 2012 23:42
ele está só colocando em evidência...
concorda que:
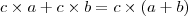
então... é o mesmo... que primeiro é feito com o

e depois com o

observe:

Tudo bem até ai? então, agora pense no

como sendo

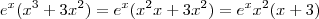
-
TheoFerraz
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite]não consigo fazer com que o denominador não de zero.
 por marcosmuscul » Ter Mar 26, 2013 12:52
por marcosmuscul » Ter Mar 26, 2013 12:52
- 2 Respostas
- 1978 Exibições
- Última mensagem por marcosmuscul

Ter Mar 26, 2013 19:48
Cálculo: Limites, Derivadas e Integrais
-
- * Trigonometria : Questões simples que não consigo fazer!!!
por Thiago Valenca » Seg Abr 16, 2012 17:38
- 4 Respostas
- 2975 Exibições
- Última mensagem por DanielFerreira

Sáb Abr 21, 2012 17:47
Trigonometria
-
- [nao consigo fazer desde o inicio] nunca fiz sozinho só
por jeffinps » Ter Fev 26, 2013 14:47
- 4 Respostas
- 2980 Exibições
- Última mensagem por jeffinps

Qua Fev 27, 2013 15:21
Cálculo: Limites, Derivadas e Integrais
-
- Eu já tentei de diversas maneiras mas o resultado dá sempre
por sergiomorales » Qui Jun 02, 2011 12:28
- 1 Respostas
- 2175 Exibições
- Última mensagem por carlosalesouza

Sáb Jun 04, 2011 02:34
Binômio de Newton
-
- Volume final
por Davip5 » Dom Jun 12, 2011 01:02
- 0 Respostas
- 1417 Exibições
- Última mensagem por Davip5

Dom Jun 12, 2011 01:02
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 14 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



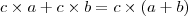
 e depois com o
e depois com o 

 como sendo
como sendo 
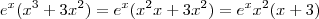



 , avisa que eu resolvo.
, avisa que eu resolvo.

