Eu não consigo desenvolver a alternativa a) da primeira questão e nem a b) da segunda. Tenho varios exercicios no mesmo modelo mas nenhum deles eu consigo, acredito que se me ajudarem com esses eu consigo desenvolver o restante. Na alternativa a) da primeira eu não consigo sair do 0. Já a b) da segunda eu começo, mas paro na hora de desenvolver o limite de
 quando
quando  . É isso ai pessoal, a alternativa b) da primeira e a a) da segunda eu consegui tranquilamente.
. É isso ai pessoal, a alternativa b) da primeira e a a) da segunda eu consegui tranquilamente.Att,
Umbrorz.


![\lim_{x\rightarrow-\infty}\frac{x(\sqrt[]{x^2-6x+1}+x)}{\sqrt[3]{8x^3-2x^2-x}+x} \lim_{x\rightarrow-\infty}\frac{x(\sqrt[]{x^2-6x+1}+x)}{\sqrt[3]{8x^3-2x^2-x}+x}](/latexrender/pictures/a61d4ddf6b5bf018d5d4963caf9cca4a.png)
![\lim_{x\rightarrow-\infty}\frac{\frac{x(\sqrt[]{x^2-6x+1}+x)}{x}{}}{\frac{\sqrt[3]{8x^3-2x^2-x}+x}{x}} \lim_{x\rightarrow-\infty}\frac{\frac{x(\sqrt[]{x^2-6x+1}+x)}{x}{}}{\frac{\sqrt[3]{8x^3-2x^2-x}+x}{x}}](/latexrender/pictures/7667117cf373378faf715e383f795039.png)
![\lim_{x\rightarrow-\infty}\frac{(\sqrt[]{x^2-6x+1}+x){}}{\sqrt[3]{8-\frac{2}{x}-\frac{1}{x^2}}+1}} \lim_{x\rightarrow-\infty}\frac{(\sqrt[]{x^2-6x+1}+x){}}{\sqrt[3]{8-\frac{2}{x}-\frac{1}{x^2}}+1}}](/latexrender/pictures/4b702b8051ad5e23088b78bc4865f387.png)
![\lim_{x\rightarrow-\infty}\frac{(\sqrt[]{1-\frac{6}{x}+\frac{1}{x^2}}+1){}}{\frac{\sqrt[3]{8-\frac{2}{x}-\frac{1}{x^2}}+1}{x}} \lim_{x\rightarrow-\infty}\frac{(\sqrt[]{1-\frac{6}{x}+\frac{1}{x^2}}+1){}}{\frac{\sqrt[3]{8-\frac{2}{x}-\frac{1}{x^2}}+1}{x}}](/latexrender/pictures/7fcb342f3f4014f69d38d3eb9bfb5ff0.png)
![\lim_{x\rightarrow-\infty}\frac{(\sqrt[]{1-0+0}+1){}}{\frac{\sqrt[3]{8-0-0}+1}{\infty}}=\infty \lim_{x\rightarrow-\infty}\frac{(\sqrt[]{1-0+0}+1){}}{\frac{\sqrt[3]{8-0-0}+1}{\infty}}=\infty](/latexrender/pictures/9dac1252cbe91dcf1f51828ded2ec557.png)

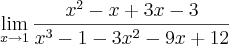

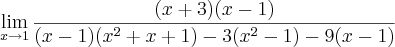
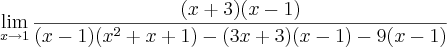

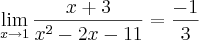


 .
.
 :
: