 por umbrorz » Dom Abr 15, 2012 00:54
por umbrorz » Dom Abr 15, 2012 00:54
Bom pessoal, tentei de todas as formar escrever as duas dúvidas que tenho, mas juro que não consegui, se alem de me ajudar na questão conseguirem me explicar como que faço os enunciados das mesma pelo tex serei grato.
Eu não consigo desenvolver a alternativa a) da primeira questão e nem a b) da segunda. Tenho varios exercicios no mesmo modelo mas nenhum deles eu consigo, acredito que se me ajudarem com esses eu consigo desenvolver o restante. Na alternativa a) da primeira eu não consigo sair do 0. Já a b) da segunda eu começo, mas paro na hora de desenvolver o limite de

quando

. É isso ai pessoal, a alternativa b) da primeira e a a) da segunda eu consegui tranquilamente.
Att,
Umbrorz.
- Anexos
-

-
umbrorz
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Abr 15, 2012 00:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ADMINISTRAÇÃO
- Andamento: cursando
 por umbrorz » Dom Abr 15, 2012 19:35
por umbrorz » Dom Abr 15, 2012 19:35
Blz cara, valeu mesmo. Vou tentar agora as outras questões parecidas. Agora eu ainda não consigo resolver a alternativa B) da segunda questão ...
-
umbrorz
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Abr 15, 2012 00:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ADMINISTRAÇÃO
- Andamento: cursando
 por umbrorz » Seg Abr 16, 2012 11:46
por umbrorz » Seg Abr 16, 2012 11:46
Alguem poderia me ajudar com a alternativa B) da segunda questão ?
-
umbrorz
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Abr 15, 2012 00:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ADMINISTRAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limites] Ajuda continuidade de função
por troziinho » Sex Nov 28, 2014 23:40
- 1 Respostas
- 1704 Exibições
- Última mensagem por adauto martins

Dom Nov 30, 2014 11:43
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITES] Dúvida em questão de Limites no infinito
 por Jacques » Ter Jul 12, 2016 21:42
por Jacques » Ter Jul 12, 2016 21:42
- 4 Respostas
- 7546 Exibições
- Última mensagem por vitor_jo

Qua Jul 13, 2016 16:51
Cálculo: Limites, Derivadas e Integrais
-
- [limites no infinito]Limite no infinito de um ponto finito
por moyses » Ter Ago 30, 2011 12:45
- 3 Respostas
- 3525 Exibições
- Última mensagem por LuizAquino

Ter Ago 30, 2011 18:57
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Limites no "infinito " prova a existência ......
por e8group » Dom Jun 17, 2012 14:37
- 2 Respostas
- 2749 Exibições
- Última mensagem por e8group

Ter Jun 19, 2012 11:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] limites no infinito
por lucasdemirand » Qui Jul 11, 2013 15:10
- 1 Respostas
- 1459 Exibições
- Última mensagem por e8group

Qui Jul 11, 2013 15:38
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 quando
quando  . É isso ai pessoal, a alternativa b) da primeira e a a) da segunda eu consegui tranquilamente.
. É isso ai pessoal, a alternativa b) da primeira e a a) da segunda eu consegui tranquilamente.

![\lim_{x\rightarrow-\infty}\frac{x(\sqrt[]{x^2-6x+1}+x)}{\sqrt[3]{8x^3-2x^2-x}+x} \lim_{x\rightarrow-\infty}\frac{x(\sqrt[]{x^2-6x+1}+x)}{\sqrt[3]{8x^3-2x^2-x}+x}](/latexrender/pictures/a61d4ddf6b5bf018d5d4963caf9cca4a.png)
![\lim_{x\rightarrow-\infty}\frac{\frac{x(\sqrt[]{x^2-6x+1}+x)}{x}{}}{\frac{\sqrt[3]{8x^3-2x^2-x}+x}{x}} \lim_{x\rightarrow-\infty}\frac{\frac{x(\sqrt[]{x^2-6x+1}+x)}{x}{}}{\frac{\sqrt[3]{8x^3-2x^2-x}+x}{x}}](/latexrender/pictures/7667117cf373378faf715e383f795039.png)
![\lim_{x\rightarrow-\infty}\frac{(\sqrt[]{x^2-6x+1}+x){}}{\sqrt[3]{8-\frac{2}{x}-\frac{1}{x^2}}+1}} \lim_{x\rightarrow-\infty}\frac{(\sqrt[]{x^2-6x+1}+x){}}{\sqrt[3]{8-\frac{2}{x}-\frac{1}{x^2}}+1}}](/latexrender/pictures/4b702b8051ad5e23088b78bc4865f387.png)
![\lim_{x\rightarrow-\infty}\frac{(\sqrt[]{1-\frac{6}{x}+\frac{1}{x^2}}+1){}}{\frac{\sqrt[3]{8-\frac{2}{x}-\frac{1}{x^2}}+1}{x}} \lim_{x\rightarrow-\infty}\frac{(\sqrt[]{1-\frac{6}{x}+\frac{1}{x^2}}+1){}}{\frac{\sqrt[3]{8-\frac{2}{x}-\frac{1}{x^2}}+1}{x}}](/latexrender/pictures/7fcb342f3f4014f69d38d3eb9bfb5ff0.png)
![\lim_{x\rightarrow-\infty}\frac{(\sqrt[]{1-0+0}+1){}}{\frac{\sqrt[3]{8-0-0}+1}{\infty}}=\infty \lim_{x\rightarrow-\infty}\frac{(\sqrt[]{1-0+0}+1){}}{\frac{\sqrt[3]{8-0-0}+1}{\infty}}=\infty](/latexrender/pictures/9dac1252cbe91dcf1f51828ded2ec557.png)

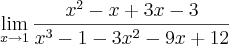

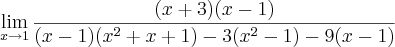
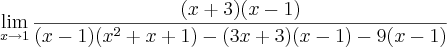

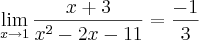



 , avisa que eu resolvo.
, avisa que eu resolvo.

