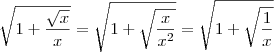por natyncb » Qui Abr 12, 2012 00:31
por natyncb » Qui Abr 12, 2012 00:31
Como solucionar esse tipo de limite com raiz??
![\lim_{x\rightarrow\infty} \sqrt[]{x +}\sqrt[]{x +}\sqrt[]{x} - \sqrt[]{x} \lim_{x\rightarrow\infty} \sqrt[]{x +}\sqrt[]{x +}\sqrt[]{x} - \sqrt[]{x}](/latexrender/pictures/c75cecf4ecdb298b02d38e536f78ea66.png)
É a minha primeira vez no fórum, estou com uma certa dificuldade para montar essa fórmula. No exemplo acima, é uma raiz dentro da outra .. No caso, os três primeiros 'x', depois vem diminuindo essa última raiz. Deu pra entender??
Estou enviando anexo uma foto que tirei do meu caderno com a fórmula correta. rs
Estou estudando Limites no período da faculdade, e deparei com esse exemplo na minha lista de exercicios.
Não sei como saio disso .. rs
- Anexos
-
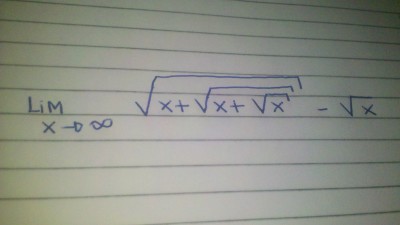
- Como resolver este tipo de Limite ?
-
natyncb
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Abr 12, 2012 00:00
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por LuizAquino » Qui Abr 12, 2012 12:33
por LuizAquino » Qui Abr 12, 2012 12:33
natyncb escreveu:Como solucionar esse tipo de limite com raiz??
![\lim_{x\rightarrow\infty} \sqrt[]{x +}\sqrt[]{x +}\sqrt[]{x} - \sqrt[]{x} \lim_{x\rightarrow\infty} \sqrt[]{x +}\sqrt[]{x +}\sqrt[]{x} - \sqrt[]{x}](/latexrender/pictures/c75cecf4ecdb298b02d38e536f78ea66.png)
É a minha primeira vez no fórum, estou com uma certa dificuldade para montar essa fórmula. No exemplo acima, é uma raiz dentro da outra .. No caso, os três primeiros 'x', depois vem diminuindo essa última raiz. Deu pra entender??
Estou enviando anexo uma foto que tirei do meu caderno com a fórmula correta. rs

- figura.jpg (7.63 KiB) Exibido 13759 vezes
Estou estudando Limites no período da faculdade, e deparei com esse exemplo na minha lista de exercicios.
Não sei como saio disso .. rs
O limite desejado é:
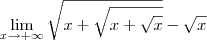
Para escrever esse limite aqui no fórum, use o código:
- Código: Selecionar todos
[tex]\lim_{x\to +\infty} \sqrt{x + \sqrt{x + \sqrt{x}}} - \sqrt{x}[/tex]
Para começar a resolver, multiplique e divida a expressão dentro do limite por
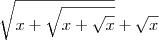
. Nesse caso, temos que:
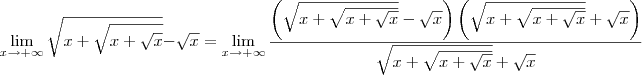
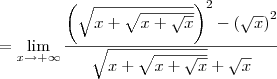

Agora divida o numerador e o denominador por

. Nesse caso, temos que:
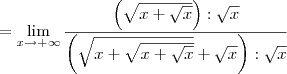
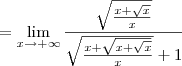

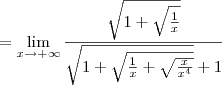
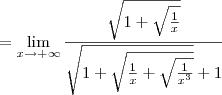
Agora tente concluir o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por natyncb » Qui Abr 12, 2012 12:45
por natyncb » Qui Abr 12, 2012 12:45
Meio caminho andando, agora vou tentar resolver aqui ..
Muito obrigada pela ajuda !
-
natyncb
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Abr 12, 2012 00:00
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por natyncb » Qui Abr 12, 2012 15:26
por natyncb » Qui Abr 12, 2012 15:26
Fiquei quebrando a cabeça aqui tentando resolver o restante da questão.
Consegui encontrar 1 como resposta.
Será que está certo, ou devo refazer tudo ?? hahaaa
-
natyncb
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Abr 12, 2012 00:00
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por LuizAquino » Qui Abr 12, 2012 17:48
por LuizAquino » Qui Abr 12, 2012 17:48
natyncb escreveu:Fiquei quebrando a cabeça aqui tentando resolver o restante da questão.
Consegui encontrar 1 como resposta.
Será que está certo, ou devo refazer tudo ??
A reposta não é 1.
Lembre-se que:
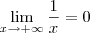
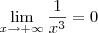
Desse modo, temos que:
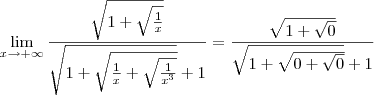

-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por doleand » Ter Ago 21, 2012 23:43
por doleand » Ter Ago 21, 2012 23:43
não consegui entender o q foi feito ao certo... se puder me esclarecer...
-
doleand
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Ter Ago 21, 2012 22:50
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia de produção
- Andamento: cursando
 por LuizAquino » Qua Ago 22, 2012 07:41
por LuizAquino » Qua Ago 22, 2012 07:41
doleand escreveu:não consegui entender o q foi feito ao certo... se puder me esclarecer...
Exatamente que parte você não entendeu?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por doleand » Qua Ago 22, 2012 16:11
por doleand » Qua Ago 22, 2012 16:11
Agora divida o numerador e o denominador por raiz de x, (desta parte em diante)
-
doleand
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Ter Ago 21, 2012 22:50
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia de produção
- Andamento: cursando
 por LuizAquino » Qui Ago 23, 2012 19:09
por LuizAquino » Qui Ago 23, 2012 19:09
doleand escreveu:Agora divida o numerador e o denominador por raiz de x, (desta parte em diante)
Pois bem, temos o seguinte limite:
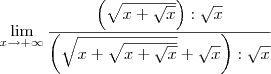
Vamos desenvolver o numerador. Note que escrever
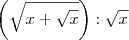
é o mesmo que escrever

. Mas lembrando de propriedades de radiciação, sabemos que

. Desse modo, temos que:

Por outro lado, sabemos que

. Desse modo, podemos escrever que:
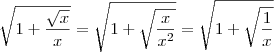
Em resumo, temos que
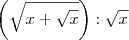
é equivalente a

Agora tente usar ideias semelhantes para desenvolver o denominador.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por doleand » Sex Ago 24, 2012 00:32
por doleand » Sex Ago 24, 2012 00:32
muito obrigada vc esclareceu algumas pendencias de anos atrás,dúvidas q eu nem sabia que tinha...valeu mesmo, brigadão!!!

-
doleand
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Ter Ago 21, 2012 22:50
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia de produção
- Andamento: cursando
 por LuizAquino » Sex Ago 24, 2012 07:50
por LuizAquino » Sex Ago 24, 2012 07:50
doleand escreveu:muito obrigada vc esclareceu algumas pendencias de anos atrás,dúvidas q eu nem sabia que tinha...valeu mesmo, brigadão!!!

Seria interessante que você fizesse uma revisão dos conteúdos de Matemática dos níveis fundamental e médio. Com certeza isso ajudará no seu aprendizado de Cálculo.
Por exemplo, assista as videoaulas "Matemática Zero - Aula 9 - Potenciação", "Matemática Zero - Aula 10 - Radiciação", "Matemática Zero - Aula 11 - Fatoração" e "Matemática Zero - Aula 12 - Racionalização". Todas essas videoaulas estão disponíveis no canal do Nerckie no YouTube:
http://www.youtube.com/nerckie
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limite - como resolver um lim quando temos raiz^2 e raiz^3.
por Monica santos » Sex Ago 16, 2013 14:22
- 4 Respostas
- 4134 Exibições
- Última mensagem por young_jedi

Sex Ago 16, 2013 19:01
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo: limite com raiz dentro de raiz
 por roberto_trebor » Sáb Fev 15, 2014 20:45
por roberto_trebor » Sáb Fev 15, 2014 20:45
- 1 Respostas
- 2240 Exibições
- Última mensagem por Man Utd

Dom Fev 16, 2014 17:58
Cálculo: Limites, Derivadas e Integrais
-
- [Radiciação] Raiz dentro de raiz
por amandasousa_m » Sex Jul 19, 2013 09:37
- 2 Respostas
- 3436 Exibições
- Última mensagem por amandasousa_m

Sex Jul 19, 2013 21:58
Equações
-
- como poderia resolver por limites?
por ronaldy » Seg Set 08, 2008 16:22
- 3 Respostas
- 6033 Exibições
- Última mensagem por admin

Ter Set 09, 2008 21:57
Cálculo: Limites, Derivadas e Integrais
-
- limites como resolver sem L'hospital
 por eulercx » Qui Jan 14, 2016 10:37
por eulercx » Qui Jan 14, 2016 10:37
- 1 Respostas
- 3880 Exibições
- Última mensagem por RuuKaasu

Qui Jan 14, 2016 18:29
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow\infty} \sqrt[]{x +}\sqrt[]{x +}\sqrt[]{x} - \sqrt[]{x} \lim_{x\rightarrow\infty} \sqrt[]{x +}\sqrt[]{x +}\sqrt[]{x} - \sqrt[]{x}](/latexrender/pictures/c75cecf4ecdb298b02d38e536f78ea66.png)


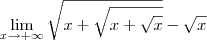
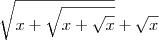 . Nesse caso, temos que:
. Nesse caso, temos que: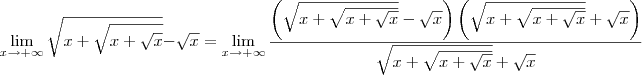
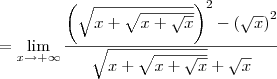

 . Nesse caso, temos que:
. Nesse caso, temos que: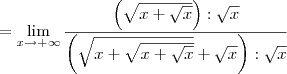
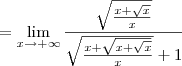

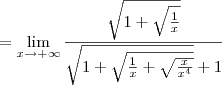
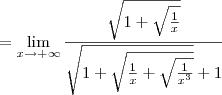

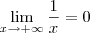
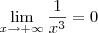
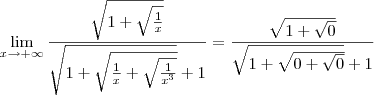

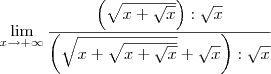
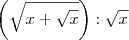 é o mesmo que escrever
é o mesmo que escrever  . Mas lembrando de propriedades de radiciação, sabemos que
. Mas lembrando de propriedades de radiciação, sabemos que  . Desse modo, temos que:
. Desse modo, temos que:
 . Desse modo, podemos escrever que:
. Desse modo, podemos escrever que: