Quais são as dimensões do retângulo de menor perímetro que tem área de 1 ha?
Já tentei encontrar a solução em 3 livros q tenho, mas os exemplos e teorias não estão me ajudando.
Peço a gentileza para ajudar-me, agradeço dede já. Muito obrigada!



Grasi escreveu:Quais são as dimensões do retângulo de menor perímetro que tem área de 1 ha?
Já tentei encontrar a solução em 3 livros q tenho, mas os exemplos e teorias não estão me ajudando.
Peço a gentileza para ajudar-me, agradeço dede já. Muito obrigada!
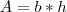 , logo,
, logo, 
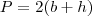
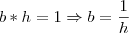 , substituindo na fórmula do perímetro:
, substituindo na fórmula do perímetro: 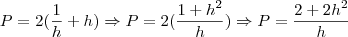
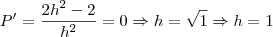 (ponto de mínimo local)
(ponto de mínimo local)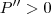 ,
, 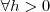 , logo o gráfico de P é côncavo para cima e o ponto de mínimo local deve ser também o mínimo absoluto.
, logo o gráfico de P é côncavo para cima e o ponto de mínimo local deve ser também o mínimo absoluto. , logo, se o retângulo tem área igual a 1, a base também deve ser igual a 1
, logo, se o retângulo tem área igual a 1, a base também deve ser igual a 1  .
.

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes


 , avisa que eu resolvo.
, avisa que eu resolvo.

