Sei calcular a maxima e minima de f(x) e usar os testes de derivada mas o mais simples como obter as raizes da função eu nao consigo!
a questão:
1. Determine os intervalos em que f(x) é crescente e decrescente, os valores de máximo e mínimo relativos de f(x), os intervalos de concavidade, os pontos de inflexão e o gráfico de f(x) utilizando os testes da 1a e da 2a derivada:
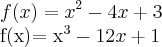
Eu queria ajuda para determinar os intervalos de f(x), mas por favor coloquem a evolucao dos calculos pois não sei fazê-los!
Obrigadaa





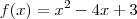
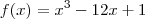
 .
.