Como deve ficar a função
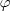 para eu deriva-la?
para eu deriva-la?Seja
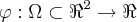 ,
,  aberto de classe C². Verefique que o Campo Vetorial
aberto de classe C². Verefique que o Campo Vetorial  é irrotacional.
é irrotacional.
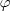 para eu deriva-la?
para eu deriva-la?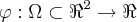 ,
,  aberto de classe C². Verefique que o Campo Vetorial
aberto de classe C². Verefique que o Campo Vetorial  é irrotacional.
é irrotacional.
carvalhothg escreveu:Seja,
aberto de classe C². Verefique que o Campo Vetorial
é irrotacional.
carvalhothg escreveu:Pessoal este é um exercicio do livro Gudorrize Calculo III, sera que alguem pode me ajudar a resolver, não estou conseguindo provar que isso é irrotacional.
Como deve ficar a funçãopara eu deriva-la?
 .
. , então temos que:
, então temos que:
 .
.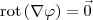 .
.
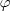 é de classe C².
é de classe C².
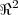

carvalhothg escreveu:Aquino,
o que quer dizer quando se diz que a função é de classe C²?
Por acaso quer dizer que ela pertence ao espaço

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes

 .
.
 :
: