 por DanielFerreira » Dom Mar 18, 2012 12:44
por DanielFerreira » Dom Mar 18, 2012 12:44
Seja
A o retângulo
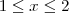
,
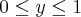
. Calcule
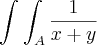
dx dy
Editado pela última vez por
DanielFerreira em Dom Mar 18, 2012 15:42, em um total de 2 vezes.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por LuizAquino » Dom Mar 18, 2012 12:47
por LuizAquino » Dom Mar 18, 2012 12:47
danjr5 escreveu:Seja
A o retângulo
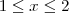
,
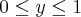
. Calcule
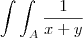
dx dy
Qual foi a sua dificuldade? Por favor, envie a sua tentativa.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por DanielFerreira » Dom Mar 18, 2012 15:43
por DanielFerreira » Dom Mar 18, 2012 15:43
danjr5 escreveu:Seja
A o retângulo
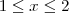
,
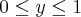
. Calcule
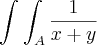
dx dy
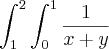
dy dx =
![\int_{1}^{2}\left[ln (x+y) dy\right]_{0}^{1} \int_{1}^{2}\left[ln (x+y) dy\right]_{0}^{1}](/latexrender/pictures/4fb7d8dfcf9aabe859365cd3d7f909d8.png)
dx =
F(1) = ln (x + 1)
F(0) = ln x
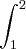
ln (x+1) - ln x dx =
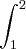
ln (x+1) dx -
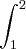
ln x dx
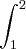
ln (x+1) dx = (x + 1) . ln (x+1) - 1
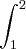
ln x dx = x . ln x - 1
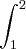
ln (x+1) - ln x dx =
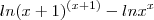
Vou ter que revisar integraçãp por partes quando a integral for definida. "x" deveria sumir, né?!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por MarceloFantini » Dom Mar 18, 2012 17:21
por MarceloFantini » Dom Mar 18, 2012 17:21
Você não avaliou nos extremos ainda.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Dom Mar 18, 2012 19:36
por LuizAquino » Dom Mar 18, 2012 19:36
danjr5 escreveu: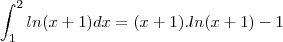
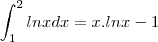
Vou ter que revisar integração por partes quando a integral for definida. "x" deveria sumir, né?!
Reveja o cálculo dessas integrais. Lembre-se que:
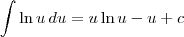
Além disso, como lembrou o colega
MarceloFantini, após determinar a antiderivada você deve aplicar os limites de integração. Ou seja, temos que:
![\int_a^b \ln u\, du = [u\ln u - u]_a^b = (b\ln b - b) - (a\ln a - a) \int_a^b \ln u\, du = [u\ln u - u]_a^b = (b\ln b - b) - (a\ln a - a)](/latexrender/pictures/b0852c1fb2fe7a12c53ef6a9700f5330.png)
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por DanielFerreira » Sex Mar 23, 2012 22:34
por DanielFerreira » Sex Mar 23, 2012 22:34
Valeu LuizAquino.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral dupla
por DanielFerreira » Sex Mar 16, 2012 23:56
- 2 Respostas
- 2862 Exibições
- Última mensagem por DanielFerreira

Sáb Mar 17, 2012 19:11
Cálculo: Limites, Derivadas e Integrais
-
- Integral dupla - 4
 por DanielFerreira » Sex Abr 06, 2012 19:49
por DanielFerreira » Sex Abr 06, 2012 19:49
- 4 Respostas
- 3116 Exibições
- Última mensagem por DanielFerreira

Sex Abr 06, 2012 21:05
Cálculo: Limites, Derivadas e Integrais
-
- Integral dupla - 5
por DanielFerreira » Sex Abr 06, 2012 20:00
- 2 Respostas
- 1903 Exibições
- Última mensagem por DanielFerreira

Sex Abr 06, 2012 20:16
Cálculo: Limites, Derivadas e Integrais
-
- Integral dupla - 6
 por DanielFerreira » Sáb Abr 14, 2012 22:54
por DanielFerreira » Sáb Abr 14, 2012 22:54
- 1 Respostas
- 1621 Exibições
- Última mensagem por LuizAquino

Dom Abr 15, 2012 23:45
Cálculo: Limites, Derivadas e Integrais
-
- Integral Dupla
por cristian9192 » Sáb Out 20, 2012 15:06
- 2 Respostas
- 1528 Exibições
- Última mensagem por cristian9192

Sáb Out 20, 2012 18:50
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
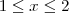 ,
, 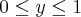 . Calcule
. Calcule 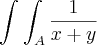 dx dy
dx dy
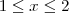 ,
, 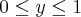 . Calcule
. Calcule 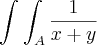 dx dy
dx dy
,
. Calcule
dx dy

,
. Calcule
dx dy
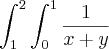 dy dx =
dy dx =![\int_{1}^{2}\left[ln (x+y) dy\right]_{0}^{1} \int_{1}^{2}\left[ln (x+y) dy\right]_{0}^{1}](/latexrender/pictures/4fb7d8dfcf9aabe859365cd3d7f909d8.png) dx =
dx =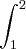 ln (x+1) - ln x dx =
ln (x+1) - ln x dx = 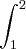 ln (x+1) dx -
ln (x+1) dx - 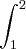 ln x dx
ln x dx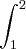 ln (x+1) dx = (x + 1) . ln (x+1) - 1
ln (x+1) dx = (x + 1) . ln (x+1) - 1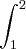 ln x dx = x . ln x - 1
ln x dx = x . ln x - 1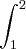 ln (x+1) - ln x dx =
ln (x+1) - ln x dx = 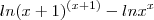


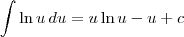
![\int_a^b \ln u\, du = [u\ln u - u]_a^b = (b\ln b - b) - (a\ln a - a) \int_a^b \ln u\, du = [u\ln u - u]_a^b = (b\ln b - b) - (a\ln a - a)](/latexrender/pictures/b0852c1fb2fe7a12c53ef6a9700f5330.png)

