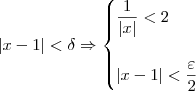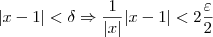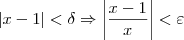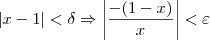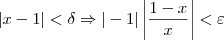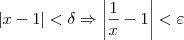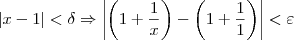MirroR escreveu:Dado uma função [f(x)=1 + 1/x] precisa-se provar que ela é contínua em p=1.
Eu já tentei várias vezes utilizar da definição elementar de continuidade |f(x)-f(p)|<


|x-p|<

para provar que a função é contínua em p=1, mas no decorrer eu não consigo associar o

ao

. Inclusive, já estou mais avançado no assunto e por outros métodos eu conseguiria provar que a função é contínua, porém é requerido o uso da definição de continuidade.
Se f é contínua em x = p, então lembre-se que você precisa provar que:
Para todo

dado, existe

tal que:

Note que você escreveu ao contrário:
MirroR escreveu: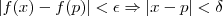
Vejamos agora o desenvolvimento. Note que:
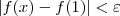
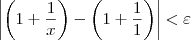
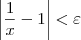
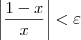
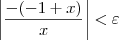
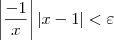
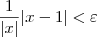
Precisamos agora determinar uma constante
c tal que
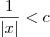
.
Como
x está próximo de 1, é razoável dizer que
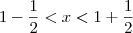
. Ou seja, temos que
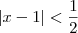
. Note que com isso já estamos escolhendo um valor
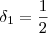
.
Além disso, também podemos dizer que
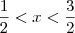
. Ou seja, temos
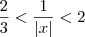
. Desse modo, temos que:
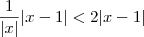
Note que se fizermos
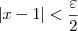
(o que significa que estamos escolhendo um
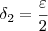
), temos que:
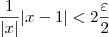
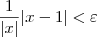
Como temos dois valores para delta (
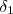
e
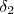
), devemos tomar o menor deles para garantir que ao mesmo tempo ocorra as duas inequações:
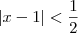
e
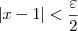
.
Isto é, vamos tomar
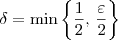
.
Agora vamos verificar que essa escolha de

funciona.
Se
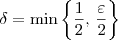
, então temos que:
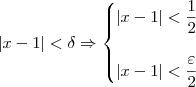
Já havíamos determinado que
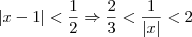
. Sendo assim, podemos dizer que:
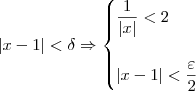
Multiplicando membro a membro as duas inequações que aparecem depois da implicação, temos que:
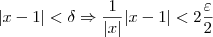
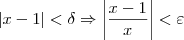
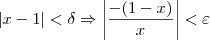
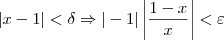
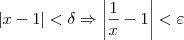
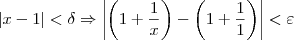


 |x-p|<
|x-p|<  para provar que a função é contínua em p=1, mas no decorrer eu não consigo associar o
para provar que a função é contínua em p=1, mas no decorrer eu não consigo associar o  ao
ao  . Inclusive, já estou mais avançado no assunto e por outros métodos eu conseguiria provar que a função é contínua, porém é requerido o uso da definição de continuidade.
. Inclusive, já estou mais avançado no assunto e por outros métodos eu conseguiria provar que a função é contínua, porém é requerido o uso da definição de continuidade.

 dado, existe
dado, existe  tal que:
tal que:
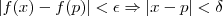
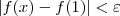
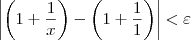
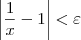
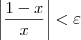
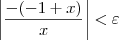
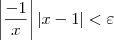
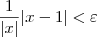
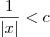 .
.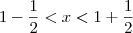 . Ou seja, temos que
. Ou seja, temos que 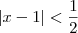 . Note que com isso já estamos escolhendo um valor
. Note que com isso já estamos escolhendo um valor 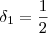 .
.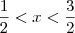 . Ou seja, temos
. Ou seja, temos 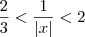 . Desse modo, temos que:
. Desse modo, temos que: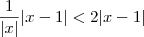
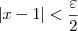 (o que significa que estamos escolhendo um
(o que significa que estamos escolhendo um 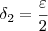 ), temos que:
), temos que: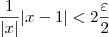
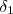 e
e 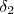 ), devemos tomar o menor deles para garantir que ao mesmo tempo ocorra as duas inequações:
), devemos tomar o menor deles para garantir que ao mesmo tempo ocorra as duas inequações: 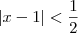 e
e 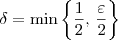 .
.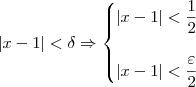
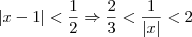 . Sendo assim, podemos dizer que:
. Sendo assim, podemos dizer que: