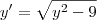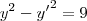por dileivas » Qua Mar 14, 2012 21:32
por dileivas » Qua Mar 14, 2012 21:32
Sinceramente, não entendi o enunciado do exercício, se alguém puder me dar uma luz de como iniciá-lo eu agradeceria muito:
É possível garantir a unicidade de solução para a equação diferencial

passando pelo ponto (1,4)? E passando pelo ponto (2, -3)? Justifique.
Obrigado! =)
-
dileivas
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Qua Mar 14, 2012 20:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências e Tecnologia / Engenharia
- Andamento: cursando
 por TheoFerraz » Qua Mar 14, 2012 22:51
por TheoFerraz » Qua Mar 14, 2012 22:51
dileivas escreveu:Sinceramente, não entendi o enunciado do exercício, se alguém puder me dar uma luz de como iniciá-lo eu agradeceria muito:
É possível garantir a unicidade de solução para a equação diferencial

passando pelo ponto (1,4)? E passando pelo ponto (2, -3)? Justifique.
Obrigado! =)
É até que simples. é possível resolver a questão sem resolver a equação até... Sempre que o exercicio pedir para "garantir a unicidade" ele quer que voce prove que só existe uma resposta (ou não). No caso ele quer que voce simplesmente verifique: "existe uma só resposta? ou não"
se voce está estudando "introdução às edo's " eu imagino que esse exercicio é teórico mesmo, não é para ser provado resolvendo a equação.
Voce conhece a ideia de "condições de contorno" ? Se sim, deve ser facil responder a pergunta:
Existe só UMA função que passa por (1,4) e resolve a equação diferencial ordinária
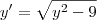
quer uma dica? outra forma de escrever a mesma equação é:
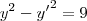
-
TheoFerraz
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
 por dileivas » Qui Mar 15, 2012 00:07
por dileivas » Qui Mar 15, 2012 00:07
Super obrigado, vou tentar resolver e já posto minha solução =D
-
dileivas
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Qua Mar 14, 2012 20:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências e Tecnologia / Engenharia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Livro EDO: Introdução às Equações Diferenciais Ordinárias
 por admin » Sáb Jul 21, 2007 19:59
por admin » Sáb Jul 21, 2007 19:59
- 2 Respostas
- 6087 Exibições
- Última mensagem por bruno_dias

Ter Set 01, 2009 01:54
Cálculo
-
- [EQUAÇÕES DIFERENCIAIS ORDINÁRIAS]
por NavegantePI » Qui Mar 02, 2017 00:43
- 0 Respostas
- 6286 Exibições
- Última mensagem por NavegantePI

Qui Mar 02, 2017 00:43
Equações
-
- [Equações Diferenciais Ordinárias e Aplicações]Duvidas
por pdss » Qua Dez 07, 2011 17:56
- 1 Respostas
- 2003 Exibições
- Última mensagem por LuizAquino

Qua Dez 07, 2011 20:14
Cálculo: Limites, Derivadas e Integrais
-
- [PROBLEMAS DE MODELAGEM] EQUAÇÕES DIFERENCIAIS ORDINÁRIAS
 por DanielGL » Ter Mai 03, 2016 14:55
por DanielGL » Ter Mai 03, 2016 14:55
- 1 Respostas
- 3244 Exibições
- Última mensagem por adauto martins

Sex Mai 06, 2016 19:12
Cálculo: Limites, Derivadas e Integrais
-
- Equações Diferencias Ordinárias- Urgente
 por leroaquino » Sáb Set 19, 2015 14:17
por leroaquino » Sáb Set 19, 2015 14:17
- 0 Respostas
- 1370 Exibições
- Última mensagem por leroaquino

Sáb Set 19, 2015 14:17
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 passando pelo ponto (1,4)? E passando pelo ponto (2, -3)? Justifique.
passando pelo ponto (1,4)? E passando pelo ponto (2, -3)? Justifique.
 passando pelo ponto (1,4)? E passando pelo ponto (2, -3)? Justifique.
passando pelo ponto (1,4)? E passando pelo ponto (2, -3)? Justifique.
passando pelo ponto (1,4)? E passando pelo ponto (2, -3)? Justifique.