![f(x)=\frac{x}{\sqrt[]{9-4x}} f(x)=\frac{x}{\sqrt[]{9-4x}}](/latexrender/pictures/23b1cca09838e84ab9fd65583b14cce1.png)
A resposta apresentada é a seguinte
![f'(x)=\frac{9-2x}{\sqrt[]{(9-4x)^3}} f'(x)=\frac{9-2x}{\sqrt[]{(9-4x)^3}}](/latexrender/pictures/af5dc59aa6b7e355c71c72bdc796ef82.png)
Desde já agradeço!

![f(x)=\frac{x}{\sqrt[]{9-4x}} f(x)=\frac{x}{\sqrt[]{9-4x}}](/latexrender/pictures/23b1cca09838e84ab9fd65583b14cce1.png)
![f'(x)=\frac{9-2x}{\sqrt[]{(9-4x)^3}} f'(x)=\frac{9-2x}{\sqrt[]{(9-4x)^3}}](/latexrender/pictures/af5dc59aa6b7e355c71c72bdc796ef82.png)

Leandro_Araujo escreveu:estou com dificuldades em derivar a seguinte função

![f'(x)=\frac{\sqrt[]{9-4x}-x\frac{1}{2}{(9-4x)}^{\frac{-1}{2}}(-4)}{({\sqrt[]{9-4x}})^{2}} f'(x)=\frac{\sqrt[]{9-4x}-x\frac{1}{2}{(9-4x)}^{\frac{-1}{2}}(-4)}{({\sqrt[]{9-4x}})^{2}}](/latexrender/pictures/6ef507e9461306c7b1805b6b678a698a.png)
![f'(x)=\frac{\sqrt[]{9-4x}+2x\frac{1}{2}{(9-4x)}^{\frac{-1}{2}}}{({\sqrt[]{9-4x}})^{2}} f'(x)=\frac{\sqrt[]{9-4x}+2x\frac{1}{2}{(9-4x)}^{\frac{-1}{2}}}{({\sqrt[]{9-4x}})^{2}}](/latexrender/pictures/3c4e301d6487a90e8b85f9ac09da9584.png)

Leandro_Araujo escreveu:Derivando pela regra do quociente:
Leandro_Araujo escreveu:
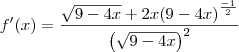
Leandro_Araujo escreveu:Dessa parte em diante não sei se eu transformo as raízes em potência...
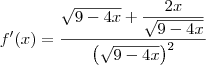
Leandro_Araujo escreveu:As vezes quando o exercício tem resposta acaba nos prejudicando, fico tentando direcionar meu raciocínio para a resposta e travo.

![f'(x)=\frac{\frac{{(\sqrt[]{9-4x}})^{2}+2x}{\sqrt[]{9-4x}}}{(\frac{\sqrt[]{9-4x}}{2})^{2}} f'(x)=\frac{\frac{{(\sqrt[]{9-4x}})^{2}+2x}{\sqrt[]{9-4x}}}{(\frac{\sqrt[]{9-4x}}{2})^{2}}](/latexrender/pictures/cf83944452a4fe7679234cc7cdfaac72.png)
 da raiz e somando com 2x e posteriormente invertendo o denominador e transformando a divisão em multiplicação encontrei:
da raiz e somando com 2x e posteriormente invertendo o denominador e transformando a divisão em multiplicação encontrei:![f'(x)=\frac{9-2x}{\sqrt[]{9-4x}}*\frac{1}{\sqrt[]{(9-4x)}}{2} f'(x)=\frac{9-2x}{\sqrt[]{9-4x}}*\frac{1}{\sqrt[]{(9-4x)}}{2}](/latexrender/pictures/ae4fb979cce9cd5790acbf7899ed6057.png)
![f'(x)=\frac{9-2x}{{\sqrt[]{(9-4x)}}^{3}} f'(x)=\frac{9-2x}{{\sqrt[]{(9-4x)}}^{3}}](/latexrender/pictures/2788a0eea83df856e922a637a961525a.png)

Leandro_Araujo escreveu:resolvendo a soma, tirei o m.m.c:
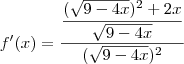
Leandro_Araujo escreveu:retirando 9-4x da raiz e somando com 2x e posteriormente invertendo o denominador e transformando a divisão em multiplicação encontrei:
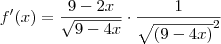
Leandro_Araujo escreveu:Encontrando enfim a resposta apresentada.
Leandro_Araujo escreveu:Bom minha dificuldade foi em complicar demais primeiro quando encontrei no denomidador uma raiz quadrada elevada a potencia 2, quis simplificar e acabou complicando o calculo.
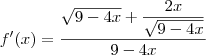
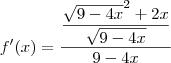
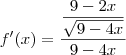
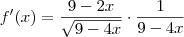
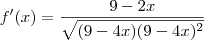
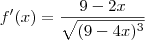
Leandro_Araujo escreveu:E aluno sempre que vê um número estranho acha que está tudo errado.
Leandro_Araujo escreveu:Bom a lista de exercicios dada por meu professor é bem extensa, vou concluí-la e acho que vai servir como uma boa revisão sobre simplificação.
Leandro_Araujo escreveu:De qualquer maneira darei uma olhada nos videos indicados.

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
