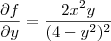por Aliocha Karamazov » Dom Fev 26, 2012 11:52
por Aliocha Karamazov » Dom Fev 26, 2012 11:52
Pessoal, o exerício é o seguinte:
Determine uma região no plano xy para o qual a equação diferencial teria uma única solução passando por um ponto
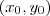
na região

Eu isolei

e ficou:
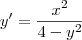
Para saber se existe solução única para uma equação diferencial, é preciso verificar dois critérios:
1. Em
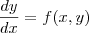
,

deve ser contínua no intervalo
2.

também deve ser contínua
Bem, calulando

cheguei à expressão:
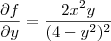
A minha dúvida é: como eu faço para encontrar a região do plano xy em que essas funções são contínuas? Eu ainda não aprendi cálculo com mais de uma variável. Na grade do meu curso, a disciplina de equações diferenciais vem antes. Isso me prejudica? Gostaria de uma ajuda. Obrigado.
-
Aliocha Karamazov
- Usuário Parceiro

-
- Mensagens: 90
- Registrado em: Qua Mar 16, 2011 17:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por LuizAquino » Dom Fev 26, 2012 13:39
por LuizAquino » Dom Fev 26, 2012 13:39
Aliocha Karamazov escreveu:Determine uma região no plano xy para o qual a equação diferencial teria uma única solução passando por um ponto (x_{0},y_{0}) na região

Eu isolei y' e ficou:
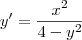
Para saber se existe solução única para uma equação diferencial, é preciso verificar dois critérios:
1. Em
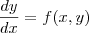
,

deve ser contínua no intervalo
2.

também deve ser contínua
Bem, calulando

cheguei à expressão:
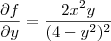
Aliocha Karamazov escreveu:como eu faço para encontrar a região do plano xy em que essas funções são contínuas?
Note que em ambas as funções, a única descontinuidade ocorre em y = 2 ou y = -2. Nesses casos, apareceria uma divisão por zero.
Sendo assim, basta tomar qualquer região do plano xy que não contenha as retas y = 2 e y = -2.
Observação: Note que não seria necessário ter feito Cálculo com várias variáveis para perceber isso.
Aliocha Karamazov escreveu:Eu ainda não aprendi cálculo com mais de uma variável. Na grade do meu curso, a disciplina de equações diferenciais vem antes. Isso me prejudica?
Isso vai depender de como a disciplina de Equações Diferenciais será organizada. Se durante a disciplina for levado em consideração que você ainda não estudou Cálculo com várias variáveis, então os conteúdos serão adaptados para essa realidade. Quando for necessário, os conceitos serão definidos.
Por exemplo, se você só sabe derivar funções de uma variável, então será necessário explicar o que significa a derivada parcial de f(x, y) em relação a y. Isto é, o que significa

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Solução de uma Equação diferencial ordinaria
por thejotta » Seg Jan 14, 2013 00:03
- 0 Respostas
- 1016 Exibições
- Última mensagem por thejotta

Seg Jan 14, 2013 00:03
Cálculo: Limites, Derivadas e Integrais
-
- [Equação diferencial] Solução incorreta?
por KleinIll » Qui Set 19, 2013 15:45
- 2 Respostas
- 1700 Exibições
- Última mensagem por KleinIll

Sáb Set 21, 2013 01:15
Cálculo: Limites, Derivadas e Integrais
-
- [Equação diferencial parcial] Ajuda para solução de EDP
por GustavoArtur » Qui Set 22, 2011 14:24
- 3 Respostas
- 2519 Exibições
- Última mensagem por GustavoArtur

Sex Set 23, 2011 12:58
Cálculo: Limites, Derivadas e Integrais
-
- [Equação Diferencial] Grau de homogeneidade e solução geral
por kayone » Dom Set 22, 2013 17:37
- 1 Respostas
- 1653 Exibições
- Última mensagem por Man Utd

Dom Jun 15, 2014 23:49
Equações
-
- [Números Complexos] Área da região do plano complexo.
por brunocav » Qua Mai 29, 2013 15:34
- 0 Respostas
- 1975 Exibições
- Última mensagem por brunocav

Qua Mai 29, 2013 15:34
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
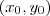 na região
na região
 e ficou:
e ficou: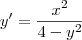
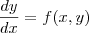 ,
,  deve ser contínua no intervalo
deve ser contínua no intervalo também deve ser contínua
também deve ser contínua cheguei à expressão:
cheguei à expressão: