Aliocha Karamazov escreveu:Determine uma região no plano xy para o qual a equação diferencial teria uma única solução passando por um ponto (x_{0},y_{0}) na região

Eu isolei y' e ficou:
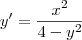
Para saber se existe solução única para uma equação diferencial, é preciso verificar dois critérios:
1. Em
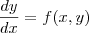
,

deve ser contínua no intervalo
2.

também deve ser contínua
Bem, calulando

cheguei à expressão:
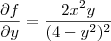
Aliocha Karamazov escreveu:como eu faço para encontrar a região do plano xy em que essas funções são contínuas?
Note que em ambas as funções, a única descontinuidade ocorre em y = 2 ou y = -2. Nesses casos, apareceria uma divisão por zero.
Sendo assim, basta tomar qualquer região do plano xy que não contenha as retas y = 2 e y = -2.
Observação: Note que não seria necessário ter feito Cálculo com várias variáveis para perceber isso.
Aliocha Karamazov escreveu:Eu ainda não aprendi cálculo com mais de uma variável. Na grade do meu curso, a disciplina de equações diferenciais vem antes. Isso me prejudica?
Isso vai depender de como a disciplina de Equações Diferenciais será organizada. Se durante a disciplina for levado em consideração que você ainda não estudou Cálculo com várias variáveis, então os conteúdos serão adaptados para essa realidade. Quando for necessário, os conceitos serão definidos.
Por exemplo, se você só sabe derivar funções de uma variável, então será necessário explicar o que significa a derivada parcial de f(x, y) em relação a y. Isto é, o que significa

.
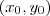 na região
na região
 e ficou:
e ficou: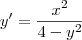
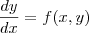 ,
,  deve ser contínua no intervalo
deve ser contínua no intervalo também deve ser contínua
também deve ser contínua cheguei à expressão:
cheguei à expressão: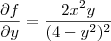





 , avisa que eu resolvo.
, avisa que eu resolvo.

