 por ARCS » Dom Fev 12, 2012 00:11
por ARCS » Dom Fev 12, 2012 00:11
Estou martelando na minha cabeça como resolver essa integral com substituição (Consegui fazer com frações parciais). Alguém ai tem alguma dica !

-
ARCS
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Qui Out 28, 2010 18:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por fraol » Dom Fev 12, 2012 10:44
por fraol » Dom Fev 12, 2012 10:44
Dá pra fazer por subsituição.
Primeiro rearranjando a expressão do integrando:

E depois substituindo:

então teremos
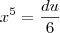
e

.
Disso aí sai a resposta.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivada: Livro Stewart
por leandro_aur » Sáb Ago 13, 2011 16:14
- 3 Respostas
- 2433 Exibições
- Última mensagem por LuizAquino

Sáb Ago 13, 2011 21:23
Cálculo: Limites, Derivadas e Integrais
-
- [Álgebra]Livro Problemas Selecionados de Matemática(Gandhi)
por PauloLima » Sáb Ago 24, 2013 17:50
- 0 Respostas
- 1875 Exibições
- Última mensagem por PauloLima

Sáb Ago 24, 2013 17:50
Álgebra Elementar
-
- Teorema de Stewart - 2ª Fórmula
por matheus_frs1 » Dom Nov 02, 2014 19:54
- 3 Respostas
- 2674 Exibições
- Última mensagem por Russman

Seg Nov 03, 2014 00:10
Geometria Plana
-
- Possível erro de digitação no Stewart 5ª edição!
por ravi » Sex Jan 18, 2013 03:11
- 2 Respostas
- 3102 Exibições
- Última mensagem por ravi

Sex Jan 18, 2013 13:15
Cálculo: Limites, Derivadas e Integrais
-
- livro de matemática
por DanielFerreira » Sex Mar 26, 2010 12:54
- 1 Respostas
- 3364 Exibições
- Última mensagem por Cleyson007

Sex Mar 26, 2010 17:23
Piadas
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






 então teremos
então teremos 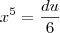 e
e  .
. 


 , avisa que eu resolvo.
, avisa que eu resolvo.

