 por Profeta » Qui Jan 26, 2012 22:08
por Profeta » Qui Jan 26, 2012 22:08
-
Profeta
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Jan 26, 2012 14:21
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura Matemática
- Andamento: cursando
 por ant_dii » Sex Jan 27, 2012 02:54
por ant_dii » Sex Jan 27, 2012 02:54
Nem precisava disso tudo.
Veja,
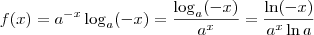
então
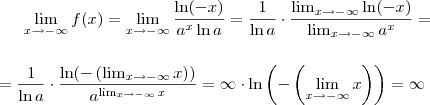
Mas para entender melhor você precisará estudar sobre Limite de função contínua, que foi a ferramenta que usei aqui...
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por LuizAquino » Sex Jan 27, 2012 20:44
por LuizAquino » Sex Jan 27, 2012 20:44
ant_dii escreveu:Veja,
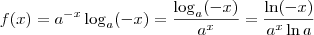
então
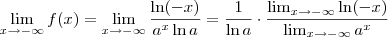
Há dois casos para analisar.
Caso 1) 0 < a < 1
Nesse caso, temos que
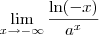
é uma indeterminação do tipo
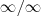
.
Aplicando a Regra de L'Hospital, temos que:
![\frac{1}{\ln a}\lim_{x\to -\infty} \frac{ [\ln(-x)]^\prime}{[a^x]^\prime} = \frac{1}{\ln a}\lim_{x\to -\infty} \frac{\frac{1}{x}}{a^x\ln a} \frac{1}{\ln a}\lim_{x\to -\infty} \frac{ [\ln(-x)]^\prime}{[a^x]^\prime} = \frac{1}{\ln a}\lim_{x\to -\infty} \frac{\frac{1}{x}}{a^x\ln a}](/latexrender/pictures/2ba608baa7ecaf1b449d2ca4cd419a34.png)
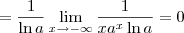 Caso 2)
Caso 2) a > 1
Nesse caso, temos que:
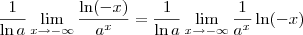
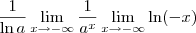
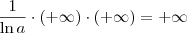
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por ant_dii » Sex Jan 27, 2012 21:24
por ant_dii » Sex Jan 27, 2012 21:24
Opa...
Valew LuizAquino...
Esqueci deste detalhe na hora de escrever... resolvi para a=2, generalizei, pois achei tranquilo fazer isso, e nem me toquei... Detalhe importante...
Mil desculpas
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por Profeta » Sáb Jan 28, 2012 10:32
por Profeta » Sáb Jan 28, 2012 10:32
obrigado pela observação da equipeé assim um por todos e todos por um.
Jesus abençoe vocês
-
Profeta
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Jan 26, 2012 14:21
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura Matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [limites] reciso de ajuda nessa questão de limites raiz quad
por alexia » Ter Nov 15, 2011 19:55
- 1 Respostas
- 5411 Exibições
- Última mensagem por LuizAquino

Qua Nov 16, 2011 15:16
Cálculo: Limites, Derivadas e Integrais
-
- [Limites]Preciso de ajuda para calcular alguns limites
por Pessoa Estranha » Ter Jul 16, 2013 17:15
- 2 Respostas
- 4759 Exibições
- Última mensagem por LuizAquino

Qua Jul 17, 2013 09:12
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Ajuda com limites no infinito e continuidade
 por umbrorz » Dom Abr 15, 2012 00:54
por umbrorz » Dom Abr 15, 2012 00:54
- 3 Respostas
- 4786 Exibições
- Última mensagem por umbrorz

Seg Abr 16, 2012 11:46
Cálculo: Limites, Derivadas e Integrais
-
- [limites] exercicio de calculo envolvendo limites
por lucasdemirand » Qua Jul 10, 2013 00:45
- 1 Respostas
- 4812 Exibições
- Última mensagem por e8group

Sáb Jul 20, 2013 13:08
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Dúvida sobre limites laterais
por Subnik » Sáb Abr 04, 2015 18:24
- 1 Respostas
- 2794 Exibições
- Última mensagem por DanielFerreira

Dom Abr 12, 2015 16:10
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
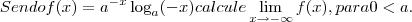
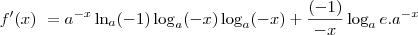

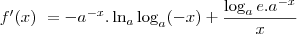

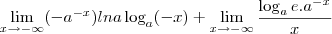

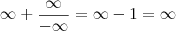

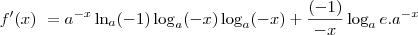

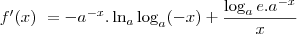

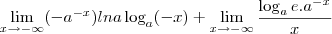

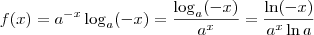
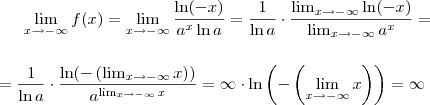

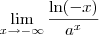 é uma indeterminação do tipo
é uma indeterminação do tipo 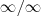 .
.![\frac{1}{\ln a}\lim_{x\to -\infty} \frac{ [\ln(-x)]^\prime}{[a^x]^\prime} = \frac{1}{\ln a}\lim_{x\to -\infty} \frac{\frac{1}{x}}{a^x\ln a} \frac{1}{\ln a}\lim_{x\to -\infty} \frac{ [\ln(-x)]^\prime}{[a^x]^\prime} = \frac{1}{\ln a}\lim_{x\to -\infty} \frac{\frac{1}{x}}{a^x\ln a}](/latexrender/pictures/2ba608baa7ecaf1b449d2ca4cd419a34.png)
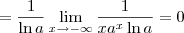
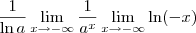
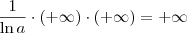





 , avisa que eu resolvo.
, avisa que eu resolvo.

