 por giboia90 » Qui Jan 05, 2012 01:50
por giboia90 » Qui Jan 05, 2012 01:50
Expresse o limite abaixo como uma derivada, e então calcule o limite.

No resultado apresenta f(x)=

e a derivada (
f '(2) = 300 ). Gostaria de saber como foi possivel obter esses resultados. passo a passo.
obrigado
-
giboia90
- Usuário Dedicado

-
- Mensagens: 32
- Registrado em: Dom Dez 04, 2011 01:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engeharia civil
- Andamento: cursando
 por LuizAquino » Qui Jan 05, 2012 10:30
por LuizAquino » Qui Jan 05, 2012 10:30
giboia90 escreveu:Expresse o limite abaixo como uma derivada, e então calcule o limite.
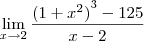
giboia90 escreveu:No resultado apresenta
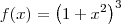
e a derivada ( f'(2) = 300 ). Gostaria de saber como foi possivel obter esses resultados. passo a passo.
Por
definição, a derivada de uma função f no ponto x=a (quando existe) é dada por:
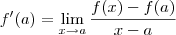
Comparando a definição com o limite dado no exercício, você deve perceber que trata-se do cálculo de f'(2), sendo que
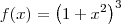
.
Agora para calcular o limite, comece usando o produto notável

.
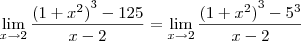
![= \lim_{x\to 2}\frac{\left(x^2 - 4\right)\left[\left(1+x^2\right)^2 + 5\left(1+x^2\right) + 25\right]}{x-2} = \lim_{x\to 2}\frac{\left(x^2 - 4\right)\left[\left(1+x^2\right)^2 + 5\left(1+x^2\right) + 25\right]}{x-2}](/latexrender/pictures/4aca0abd9bc1ae6a867a555db1d48290.png)
Agora tente terminar o exercício usando o produto notável
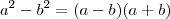
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por giboia90 » Qui Jan 05, 2012 10:59
por giboia90 » Qui Jan 05, 2012 10:59
ea derivada que resulta apos o calculo em que f'(2)= 300
-
giboia90
- Usuário Dedicado

-
- Mensagens: 32
- Registrado em: Dom Dez 04, 2011 01:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engeharia civil
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [LIMITE] DERIVADA
por beel » Seg Set 19, 2011 00:03
- 2 Respostas
- 1119 Exibições
- Última mensagem por beel

Dom Out 16, 2011 17:08
Cálculo: Limites, Derivadas e Integrais
-
- Derivada pela definição de limite
por SheylaTamarossi » Dom Jun 12, 2011 11:27
- 6 Respostas
- 8320 Exibições
- Última mensagem por Fabio Cabral

Seg Jun 13, 2011 12:07
Cálculo: Limites, Derivadas e Integrais
-
- Derivada pela definição de limite
por Andreyan » Ter Jul 12, 2011 17:55
- 4 Respostas
- 2808 Exibições
- Última mensagem por LuizAquino

Qua Jul 13, 2011 15:27
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITE] derivada de funções trigonometricas
por beel » Qua Set 21, 2011 13:09
- 3 Respostas
- 2618 Exibições
- Última mensagem por beel

Dom Out 16, 2011 17:07
Cálculo: Limites, Derivadas e Integrais
-
- [Limite, Continuidade, Derivada] Bibliografias básicas
por danielbrisolara » Ter Out 02, 2012 07:12
- 5 Respostas
- 4174 Exibições
- Última mensagem por danielbrisolara

Qua Out 03, 2012 07:47
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

 e a derivada ( f '(2) = 300 ). Gostaria de saber como foi possivel obter esses resultados. passo a passo.
e a derivada ( f '(2) = 300 ). Gostaria de saber como foi possivel obter esses resultados. passo a passo.

 e a derivada ( f '(2) = 300 ). Gostaria de saber como foi possivel obter esses resultados. passo a passo.
e a derivada ( f '(2) = 300 ). Gostaria de saber como foi possivel obter esses resultados. passo a passo.
e a derivada ( f'(2) = 300 ). Gostaria de saber como foi possivel obter esses resultados. passo a passo.
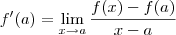
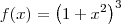 .
. .
.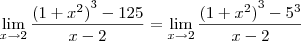
![= \lim_{x\to 2}\frac{\left(x^2 - 4\right)\left[\left(1+x^2\right)^2 + 5\left(1+x^2\right) + 25\right]}{x-2} = \lim_{x\to 2}\frac{\left(x^2 - 4\right)\left[\left(1+x^2\right)^2 + 5\left(1+x^2\right) + 25\right]}{x-2}](/latexrender/pictures/4aca0abd9bc1ae6a867a555db1d48290.png)
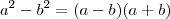 .
.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.