(sei que é produto indeterminado, mas não o tipo)
por L'hospital:

Me perco no meio!



Thamc escreveu:Tenho um exercício de cálculo que sempre chego na mesma resposta, mas acho que errei algo no meio e está errado.
(sei que é produto indeterminado, mas não o tipo)
por L'hospital:
Me perco no meio!


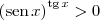 quando
quando 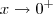 , temos que deve ocorrer
, temos que deve ocorrer  . Vamos fazer a suposição de que L seja não nulo, isto é, que temos apenas
. Vamos fazer a suposição de que L seja não nulo, isto é, que temos apenas  . Desse modo, podemos aplicar o logaritmo natural em ambos os membros da equação acima:
. Desse modo, podemos aplicar o logaritmo natural em ambos os membros da equação acima:![\ln L = \ln \left[\lim_{x\to 0^+} \left(\textrm{sen}\, x\right)^{\textrm{tg}\, x}\right] \ln L = \ln \left[\lim_{x\to 0^+} \left(\textrm{sen}\, x\right)^{\textrm{tg}\, x}\right]](/latexrender/pictures/040d1094e32ac249a461c45ea3999f9d.png)
![\ln L = \lim_{x\to 0^+} \ln \left[\left(\textrm{sen}\, x\right)^{\textrm{tg}\, x}\right] \ln L = \lim_{x\to 0^+} \ln \left[\left(\textrm{sen}\, x\right)^{\textrm{tg}\, x}\right]](/latexrender/pictures/5a1da8646623abd46d181a5916b8a4eb.png)


![\ln L = \lim_{x\to 0^+} \frac{\left[\ln \left(\textrm{sen}\, x\right)\right]^\prime}{\left(\frac{1}{\textrm{tg}\, x}\right)^\prime} \ln L = \lim_{x\to 0^+} \frac{\left[\ln \left(\textrm{sen}\, x\right)\right]^\prime}{\left(\frac{1}{\textrm{tg}\, x}\right)^\prime}](/latexrender/pictures/e74c4e853557adac2d43640504f36e46.png)
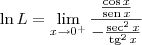

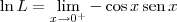


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes

 .
.
 :
: