 por beel » Dom Nov 27, 2011 18:06
por beel » Dom Nov 27, 2011 18:06
nessa integral
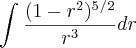
fiz r=sen

dr=cos

d

...
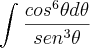
,
mas ai travei...
tentei resolver mas deu um resultado estranho
![\sqrt[]{lnx}+k \sqrt[]{lnx}+k](/latexrender/pictures/d180bccd7cf2aa1350602a6b35eb6ae8.png)
=
![\sqrt[]{lnsen \theta}+k \sqrt[]{lnsen \theta}+k](/latexrender/pictures/db642c098210df695c26b072c84d7940.png)
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Ter Nov 29, 2011 15:11
por LuizAquino » Ter Nov 29, 2011 15:11
beel escreveu:nessa integral
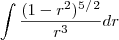
fiz
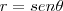
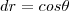
...
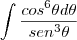
,
mas ai travei...
tentei resolver mas deu um resultado estranho
![\sqrt[]{lnx}+k= \sqrt[]{lnsen \theta}+k \sqrt[]{lnx}+k= \sqrt[]{lnsen \theta}+k](/latexrender/pictures/88d459c3adfc6eaa1415c5eeaf21be1a.png)
Note que:
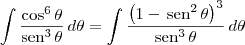
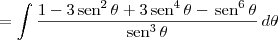
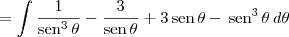
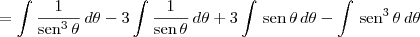
Agora basta resolver cada uma das integrais.
Lembre-se que para conferir a sua reposta você pode usar o procedimento que já foi lhe indicado
em suas mensagens anteriores.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [calculo] integral - substituiçao trigonometrica
por beel » Dom Nov 27, 2011 17:30
- 1 Respostas
- 1806 Exibições
- Última mensagem por LuizAquino

Seg Nov 28, 2011 16:19
Cálculo: Limites, Derivadas e Integrais
-
- Integral por substituição trigonométrica.
por ClaudioSP » Qui Out 08, 2009 12:25
- 1 Respostas
- 3756 Exibições
- Última mensagem por ClaudioSP

Qui Out 08, 2009 14:25
Cálculo: Limites, Derivadas e Integrais
-
- integral por substituiçao trigonometrica 3
por beel » Dom Nov 27, 2011 18:24
- 3 Respostas
- 2903 Exibições
- Última mensagem por LuizAquino

Seg Nov 28, 2011 16:44
Cálculo: Limites, Derivadas e Integrais
-
- integral- substituiçao trigonometrica 4
por beel » Dom Nov 27, 2011 18:29
- 1 Respostas
- 2062 Exibições
- Última mensagem por LuizAquino

Seg Nov 28, 2011 16:26
Cálculo: Limites, Derivadas e Integrais
-
- Integral por substituição trigonométrica
por Crist » Seg Nov 12, 2012 20:46
- 1 Respostas
- 1488 Exibições
- Última mensagem por e8group

Qui Nov 15, 2012 15:38
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
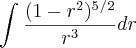
 dr=cos
dr=cos d
d
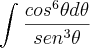 ,
,![\sqrt[]{lnx}+k \sqrt[]{lnx}+k](/latexrender/pictures/d180bccd7cf2aa1350602a6b35eb6ae8.png) =
= ![\sqrt[]{lnsen \theta}+k \sqrt[]{lnsen \theta}+k](/latexrender/pictures/db642c098210df695c26b072c84d7940.png)

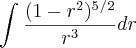
 dr=cos
dr=cos d
d
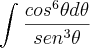 ,
,![\sqrt[]{lnx}+k \sqrt[]{lnx}+k](/latexrender/pictures/d180bccd7cf2aa1350602a6b35eb6ae8.png) =
= ![\sqrt[]{lnsen \theta}+k \sqrt[]{lnsen \theta}+k](/latexrender/pictures/db642c098210df695c26b072c84d7940.png)

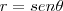
,
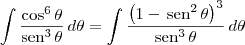
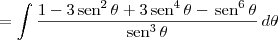
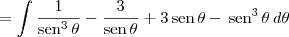
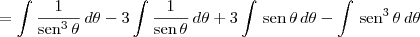


 .
.
 :
: