 por beel » Dom Nov 20, 2011 22:46
por beel » Dom Nov 20, 2011 22:46
A função y(x) tem como sua derivada 2/x + 1/x² e seu grafico passa pelo ponto P=(1,2)...assim, qual seria y(1)...
Fiz essa problema pelo PVI, integrando os dois lados da equação que ficou assim
y(x) = 2lnx - 1/x + k , sendo k=3
assim, y(1) = 2
mas o resultado nao bate com nenhuma alternativa...
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Seg Nov 21, 2011 10:16
por LuizAquino » Seg Nov 21, 2011 10:16
beel escreveu:A função y(x) tem como sua derivada 2/x + 1/x² e seu grafico passa pelo ponto P=(1,2)...assim, qual seria y(1)...
beel escreveu:Fiz essa problema pelo PVI, integrando os dois lados da equação que ficou assim
y(x) = 2lnx - 1/x + k , sendo k=3
assim, y(1) = 2
Reveja o texto do exercício, pois nem precisaria fazer cálculo algum para saber que y(1)=2. Afinal de contas, foi informado que o gráfico de y(x) passa pelo ponto P=(1, 2).
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por beel » Seg Nov 21, 2011 17:23
por beel » Seg Nov 21, 2011 17:23
Sim, eu percebi isso, mas mesmo assim, errei em alguma coisa e queria saber onde
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Seg Nov 21, 2011 21:09
por LuizAquino » Seg Nov 21, 2011 21:09
beel escreveu:Sim, eu percebi isso, mas mesmo assim, errei em alguma coisa e queria saber onde
Não há erro no que você fez. Afinal de contas, a função
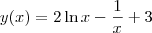
atende as duas condições do exercício:
(i) "(...)
sua derivada 2/x + 1/x² (...)"
(ii) "(...)
seu gráfico passa pelo ponto P=(1, 2) (...)"
Como eu já falei antes, você deve rever o texto do exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por beel » Ter Nov 22, 2011 15:04
por beel » Ter Nov 22, 2011 15:04
O problema é que as alternativas pra resposta, todas contem e
1)2+ 1/e
2) 2-1/e
3)2 - 5/e
4)5 + 1/e
5)5 -1/e
e minha resposta deu 2
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Ter Nov 22, 2011 15:25
por LuizAquino » Ter Nov 22, 2011 15:25
beel escreveu:O problema é que as alternativas pra resposta, todas contem e
1)2+ 1/e
2) 2-1/e
3)2 - 5/e
4)5 + 1/e
5)5 -1/e
e minha resposta deu 2
Como eu já falei antes,
você deve rever o texto do exercício.
Muito provavelmente houve um erro de digitação. O texto correto deveria ser algo como:
"
A função y(x) tem como sua derivada 2/x + 1/x² e seu gráfico passa pelo ponto P=(1,2). Sendo assim, quanto seria y(e)?"
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por beel » Ter Nov 22, 2011 15:55
por beel » Ter Nov 22, 2011 15:55
O enunciado do problema diz exatamente o seguinte:
"Considere a função y(x) cuja derivada é 2/x + 1/x² e cujo grafico passa pelo ponto P=(1,2).Então o valor de y(1) é igual a:"
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Ter Nov 22, 2011 17:06
por LuizAquino » Ter Nov 22, 2011 17:06
beel escreveu:O enunciado do problema diz exatamente o seguinte:
"Considere a função y(x) cuja derivada é 2/x + 1/x² e cujo grafico passa pelo ponto P=(1,2). Então o valor de y(1) é igual a:"
Considerando que as alternativas são aquelas que você enviou anteriormente, então o enunciado do exercício está errado.
Ou seja, houve um erro de digitação no local onde você encontrou esse exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por beel » Dom Nov 27, 2011 15:15
por beel » Dom Nov 27, 2011 15:15
Realmente, agora concertaram o exercicio, a pergunta é qual é y(e)... a resposta seria 5 - 1/e?
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Dom Nov 27, 2011 19:05
por LuizAquino » Dom Nov 27, 2011 19:05
beel escreveu:Realmente, agora concertaram o exercicio, a pergunta é qual é y(e)...
Pois é. Eu lhe avisei diversas vezes que o enunciado estava errado, mas você pareceu não acreditar.
beel escreveu:a resposta seria 5 - 1/e?
Sim.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por beel » Dom Nov 27, 2011 19:28
por beel » Dom Nov 27, 2011 19:28
no começo nao tinha entendi direito o que estava querendo dizer,porque tinha escrito o enunciado como estava direitinho, pensei que estava falando que eu tinha postado o enunciado errado, mas enfim...obrigada.
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Calculo]Alguém me ajuda nessa questão de calculo pfv.
por moeni » Seg Abr 04, 2022 21:54
- 0 Respostas
- 6488 Exibições
- Última mensagem por moeni

Seg Abr 04, 2022 21:54
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] calculo de integral - coordenada esferica
por fatalshootxd » Ter Mar 31, 2015 00:43
- 1 Respostas
- 4525 Exibições
- Última mensagem por adauto martins

Sáb Abr 04, 2015 16:13
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo] Cálculo Polinômio Interpolador
 por barbara-rabello » Qui Out 22, 2015 20:07
por barbara-rabello » Qui Out 22, 2015 20:07
- 1 Respostas
- 2653 Exibições
- Última mensagem por adauto martins

Sáb Out 24, 2015 11:00
Cálculo: Limites, Derivadas e Integrais
-
- [Calculo] Exercícios de Calculo
por Thomas » Seg Mai 16, 2016 16:39
- 0 Respostas
- 0 Exibições
- Última mensagem por Visitante

Qua Dez 31, 1969 22:00
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo: Limites, Derivadas e Integrais] Cálculo de limites
por jeferson lopes » Ter Mar 26, 2013 08:49
- 2 Respostas
- 5559 Exibições
- Última mensagem por jeferson lopes

Ter Mar 26, 2013 11:52
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



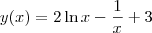 atende as duas condições do exercício:
atende as duas condições do exercício:

 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.