
- Se
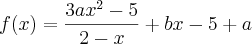 , calcule a e b de modo que:
, calcule a e b de modo que:1)
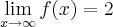
2)
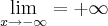


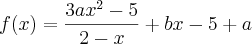 , calcule a e b de modo que:
, calcule a e b de modo que: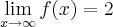
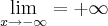

carvalhothg escreveu:Como resolvo este limite para encontrar os valores de a e b. Não estou conseguindo, sempre chego na indeterminação de
carvalhothg escreveu: Se, calcule a e b de modo que:
carvalhothg escreveu:1)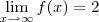
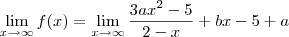
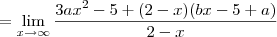
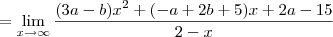
![\lim_{x\to \infty} \frac{(- a + 2b + 5)x + 2a - 15}{2-x} = \lim_{x\to \infty} \frac{[(- a + 2b + 5)x + 2a - 15]:x}{(2-x):x} \lim_{x\to \infty} \frac{(- a + 2b + 5)x + 2a - 15}{2-x} = \lim_{x\to \infty} \frac{[(- a + 2b + 5)x + 2a - 15]:x}{(2-x):x}](/latexrender/pictures/510cc53bdff32e22684e38d72ddf7cc9.png)
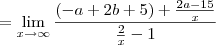
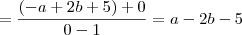
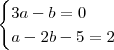
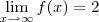
carvalhothg escreveu:2)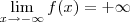
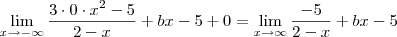
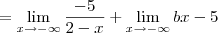
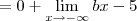
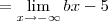
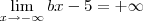
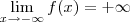

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 12 visitantes