 por procyon » Ter Nov 01, 2011 00:34
por procyon » Ter Nov 01, 2011 00:34
Olá pessoal, sou novo aqui, já tive uma participação resolvendo uma dúvida de ou outro colega, agora é a minha vez de pedir uma ajuda. É o seguinte, tenho :
![\int_{0}^{1} \frac{x}{\sqrt[2][4 -3x^{4}]} dx \int_{0}^{1} \frac{x}{\sqrt[2][4 -3x^{4}]} dx](/latexrender/pictures/38d2525d8c07692411687f9d2a7625dc.png)
Não consigo chegar em uma substituição apropriada do tipo u=função que facilite o meu trabalho na integração
Já tentei usar como variável auxiliar u o denominador completo (raíz inclusa) , com o denominador sem a raíz, ou apenas o
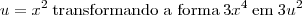
Nenhuma dessas idéias resolveu o meu problema.
Grato.
Editado pela última vez por
procyon em Ter Nov 01, 2011 21:47, em um total de 1 vez.
-
procyon
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Seg Out 31, 2011 23:40
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Ter Nov 01, 2011 12:21
por LuizAquino » Ter Nov 01, 2011 12:21
procyon escreveu:Olá pessoal, sou novo aqui, já tive uma participação resolvendo uma dúvida de ou outro colega, agora é a minha vez de pedir uma ajuda.
Seja bem-vindo ao fórum.
procyon escreveu:
Não consigo chegar em uma substituição apropriada do tipo u=função que facilite o meu trabalho na integração
Use a substituição trigonométrica

e

.
Com essa substituição, quando

, note que

. Já quando

, note que
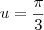
.
Dessa forma, temos que:

Agora termine o exercício.
ObservaçãoSe você desejar revisar a técnica de substituição trigonométrica, então eu recomendo que você assista a vídeo-aula "37. Cálculo I - Integração por Substituição Trigonométrica". Ela está disponível em meu canal no YouTube:
http://www.youtube.com/LCMAquino
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por procyon » Ter Nov 01, 2011 21:46
por procyon » Ter Nov 01, 2011 21:46
-
procyon
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Seg Out 31, 2011 23:40
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Estou com dificuldade para resolver esta integral
por Paulo Perez » Qui Out 03, 2013 12:22
- 2 Respostas
- 4611 Exibições
- Última mensagem por Paulo Perez

Sex Out 04, 2013 16:32
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL] Integral por partes! Alguem pode me ajudar?
por mih123 » Qua Jan 16, 2013 20:18
- 3 Respostas
- 4575 Exibições
- Última mensagem por adauto martins

Qua Out 22, 2014 09:11
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Resolver Integral definida com trigonometria
por rodrigoboreli » Dom Set 07, 2014 01:02
- 1 Respostas
- 4342 Exibições
- Última mensagem por adauto martins

Sex Out 17, 2014 12:39
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Qua Ago 17, 2011 22:33
- 2 Respostas
- 2839 Exibições
- Última mensagem por ewald

Qui Ago 18, 2011 00:54
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Sáb Ago 20, 2011 17:20
- 2 Respostas
- 2864 Exibições
- Última mensagem por LuizAquino

Dom Ago 21, 2011 21:14
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{0}^{1} \frac{x}{\sqrt[2][4 -3x^{4}]} dx \int_{0}^{1} \frac{x}{\sqrt[2][4 -3x^{4}]} dx](/latexrender/pictures/38d2525d8c07692411687f9d2a7625dc.png)
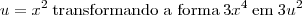



 e
e  .
. , note que
, note que  . Já quando
. Já quando  , note que
, note que 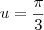 .
.


![\int_{0}^{1} \frac{x.dx}{\sqrt[2]{4 -3x^{4}}} \int_{0}^{1} \frac{x.dx}{\sqrt[2]{4 -3x^{4}}}](/latexrender/pictures/3ac543f4980a7efcc55d6a9983eb8d0a.png)
![\int_{0}^{1} \frac{x.dx}{\sqrt[2]{a^{2} - u^{2}}} \int_{0}^{1} \frac{x.dx}{\sqrt[2]{a^{2} - u^{2}}}](/latexrender/pictures/9f14739db4dee2052cf907e194305475.png)
![\nu = \sqrt[2]{3}.x^{2} \:\:\: \text{d}\nu=2x\sqrt[2]{3} \text{dx} \nu = \sqrt[2]{3}.x^{2} \:\:\: \text{d}\nu=2x\sqrt[2]{3} \text{dx}](/latexrender/pictures/2074a0a25e48bb09ce20b3873fe994af.png) , a = 2 e ficamos com uma primitiva
, a = 2 e ficamos com uma primitiva 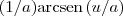


![\int_{0}^{1} \frac{x}{\sqrt{4 -3x^{4}}}\,dx = \int_0^{\frac{\pi}{3}} \frac{1}{2\sqrt{3}}\,du = \left[\frac{u}{2\sqrt{3}}\right]_0^{\frac{\pi}{3}} = \frac{\pi}{6\sqrt{3}} \int_{0}^{1} \frac{x}{\sqrt{4 -3x^{4}}}\,dx = \int_0^{\frac{\pi}{3}} \frac{1}{2\sqrt{3}}\,du = \left[\frac{u}{2\sqrt{3}}\right]_0^{\frac{\pi}{3}} = \frac{\pi}{6\sqrt{3}}](/latexrender/pictures/8c224734ffd82c0b90009ff5836acf1b.png)
