03.(UFPE) Quatro cargas elétricas puntiformes, de intensidades Q e q, estão fixas nos vértices de um quadrado, sabendo que as cargas Q estão nos vértices 1 e 3 e as cargas q nos vértices 2 e 4. Determine a razão Q/q para que a força sobre cada uma das cargas Q seja nula.
Fórmula:
F = K q Q / d²
Se Q e q tiverem mesmo sinal, todas as cargas vão se repelir uma das outras, e portanto, a força nunca será nula. Provavelmente Q e q vão ter sinais contrários. É a única forma de haver um equilíbrio de forças. Já podemos afirmar, portanto e sem medo, que Q/q é sempre negativo.
Antes de tudo quero dar nume as cargas, será A, B, C e D, onde a carga A está no vértice 1, a carga B está no vertice 2, a carga C está no vértice 3 e a carga D está no vértice 4.
Vamos pensar somente na carga A. Vamos colocar o quadrado num plano cartesiano tal que A esteja na origem do meu plano. Podemos escrever as coordenadas das minhas cargas como sendo:
A = (0,0)
B = (d,0)
C = (d,d)
D = (0,d)
Com isso via GA é muito facil determinar qual é a distancia entre as cargas, bastando encontrar o modulo dos vetores convenientes. Note que o vetor AC tem módulo, por definição, |AC| =
![\sqrt[2]{{d}^{2}+{d}^{2}} = \sqrt[2]{2}.d](/latexrender/pictures/45c91b5e43b809d2ed7b08b53600e2f8.png "\sqrt[2]{{d}^{2}+{d}^{2}} = \sqrt[2]{2}.d")
. Pode ser dele que vem a raiz quadrada da resposta.
Mas o grande problema não é esse.
É estudar as forças que atuam em uma carga qualquer.
Vamos estudar a carga A e ver se só estudando ela conseguimos chegar em Q/q. Ela recebe influencia de tres forças neste sistema: a força elétrica das cargas B,C e D.
B e D é facil determinar porque B está no eixo x e D está no eixo y, basta aplicar a formula.
O problema é a força C, que está na diagonal neste referencial! Resolver problemas de vetores na diagonal é relativamente simples: decomponha o vetor nos eixos, utilizando ferramentas de GA, mais precisamente, projeção ortogonal, e realize as analises tanto para o eixo x quanto para o eixo y.
Será mais ou menos assim:
Vamos supor que q > 0 e Q < 0, assim, entre as cargas A e D há atração,A e B há atração, e A e C há repulsão. Observe que se q <0 e Q>0, também teriamos a mesma situação. Dessa forma, para haver equilibrio a somatória de todas as forças deve ser zero. São três forças que podemos decompor nos eixos x e y, e assim, para haver equilivrio, a somatória de todas as forças em cada eixo deve ser zero.
Antes de mais nada vamos dar nomes as variaveis força. Força que B exerce em A, vamos chamar de Fb. A força que C exerce em A vamos chamar de Fc, e a força que D exerce em A, vamos chamar de Fd.
Agora, vamos pensar no eixo x, e ver se apartir dele chegamos na tão esperada razão Q/q:
Por hipótese, há equilibrio, e portanto, força da carga B + Força da carga C decomposta no eixo x = 0
Analisando o sinal das forças, a força B está no sentido positivo de x, por causa da atração. A força C em x está no sentido negativo de x. Podemos então escrever que
|Fb| - |Fc x| = 0 e portanto, |Fb| = |Fc em x|
Para de decompor a força Fc no eixo x, basta conhecer o angulo da diagonal, sabemos que vale pi/4
Fc x = Fc sen(pi/4)
Fc x = Fc
![\frac{\sqrt[2]{2}}{2}](/latexrender/pictures/087ef0498ec0056debd92518bfa3944e.png "\frac{\sqrt[2]{2}}{2}")
Assim, aplicando a formula no eixo x, temos que,
|Fb| = |Fc em x|
![\frac{kQq}{d²} = \frac{kQ²}{{\left(d \sqrt[2]{2} \right)}^{2}} \frac{\sqrt[2]{2}}{2} \Rightarrow \frac{kQq}{d²} = \frac{kQ²}{2{d}^{2}} \frac{\sqrt[2]{2}}{2} \Rightarrow \frac{q}{1} = \frac{Q}{2} \frac{\sqrt[2]{2}}{2} \Rightarrow \frac{Q}{q} = \frac{4}{\sqrt[2]{2}} \Rightarrow \frac{Q}{q} = \frac{4}{\sqrt[2]{2}} \frac{\sqrt[2]{2}}{\sqrt[2]{2}} \Rightarrow 2\sqrt[2]{2}](/latexrender/pictures/b5d8e837279a202348d3f86a4449e81d.png "\frac{kQq}{d²} = \frac{kQ²}{{\left(d \sqrt[2]{2} \right)}^{2}} \frac{\sqrt[2]{2}}{2} \Rightarrow \frac{kQq}{d²} = \frac{kQ²}{2{d}^{2}} \frac{\sqrt[2]{2}}{2} \Rightarrow \frac{q}{1} = \frac{Q}{2} \frac{\sqrt[2]{2}}{2} \Rightarrow \frac{Q}{q} = \frac{4}{\sqrt[2]{2}} \Rightarrow \frac{Q}{q} = \frac{4}{\sqrt[2]{2}} \frac{\sqrt[2]{2}}{\sqrt[2]{2}} \Rightarrow 2\sqrt[2]{2}")
Obersve que encontramos Q/q em módulo. Falta fazer a análise do sinal, aliás, ja foi feito, para que hava equilíbrio q>0 e Q<0... ou q<0 e Q>0, é por isso que Q/q < 0 sempre!
A resposta fica - 2 raiz 2
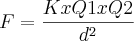
![-2\sqrt[2]{2}](/latexrender/pictures/304901268dcb59562de386577264462a.png "-2\sqrt[2]{2}")
por 
, seja verdadeira:
(hipótese da indução)
seja verdadeiro, e pretendemos provar que também é verdadeiro para 
.
é 
a 
, e este por sua vez é sempre 
que 
, logo:
