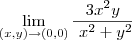
Encurtando passos afirmo que esse limite precisa ser calculado pela definição, ou seja,
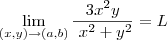 se
se  sempre que (x,y)
sempre que (x,y)  D e
D e 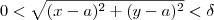 . Economizando passos temos que o candidato ao limite é 0 e o ponto (a,b)=(0,0) então temos:
. Economizando passos temos que o candidato ao limite é 0 e o ponto (a,b)=(0,0) então temos: sempre que
sempre que 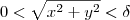
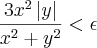 sempre que
sempre que 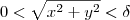 . Mas
. Mas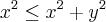 para
para  .
.Logo.

Assim (não entendo o que ele faz abaixo).
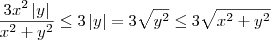
de onde vem que
 .
.Sei que pode estar claro para muitos mas fico um pouco perdido com alguns passos.
Grato Flávio Santana.



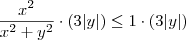
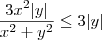
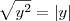 . Temos então que:
. Temos então que: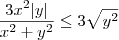
 para qualquer real
para qualquer real 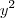 em ambos os lados, temos que
em ambos os lados, temos que 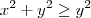 , para qualquer real
, para qualquer real  .
.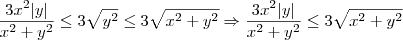
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.