 por ericamila2 » Sáb Out 15, 2011 18:15
por ericamila2 » Sáb Out 15, 2011 18:15
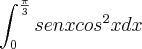
tem que dar no final =
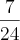
então?
-
ericamila2
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sáb Set 24, 2011 22:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Análise de sistemas
- Andamento: cursando
 por LuizAquino » Sáb Out 15, 2011 19:06
por LuizAquino » Sáb Out 15, 2011 19:06
Qual foi o resultado que você encontrou para a integral indefinida? Isto é, qual foi a primitiva para
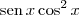
que você encontrou?
Se você precisar revisar como calcular integrais com produto entre potências de seno e cosseno, então eu recomendo que você assista a vídeo-aula "32. Cálculo I - Integral de Produto entre Potências de Seno e Cosseno". Ela está disponível em meu canal no YouTube:
http://www.youtube.com/LCMAquino
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- senx
por camilaarbar » Qua Mai 13, 2009 21:57
- 3 Respostas
- 1963 Exibições
- Última mensagem por Cleyson007

Sáb Mai 16, 2009 15:24
Trigonometria
-
- derivada x^(x^senx)
por paula luna » Ter Jun 07, 2011 15:15
- 4 Respostas
- 2420 Exibições
- Última mensagem por paula luna

Sex Jun 10, 2011 04:48
Cálculo: Limites, Derivadas e Integrais
-
- a primitiva senx dx
por Ana Maria da Silva » Sex Nov 29, 2013 08:52
- 2 Respostas
- 1385 Exibições
- Última mensagem por Ana Maria da Silva

Sáb Nov 30, 2013 08:20
Cálculo: Limites, Derivadas e Integrais
-
- o domínio da função z=f(x,y)=(x?y)/(senx?seny)
por eduardo_ochoa » Sex Set 08, 2017 17:13
- 0 Respostas
- 2590 Exibições
- Última mensagem por eduardo_ochoa

Sex Set 08, 2017 17:13
Funções
-
- [Integral] Estou com dificuldade para resolver esta integral
por Paulo Perez » Qui Out 03, 2013 12:22
- 2 Respostas
- 4611 Exibições
- Última mensagem por Paulo Perez

Sex Out 04, 2013 16:32
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
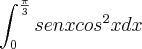
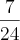

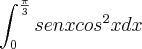
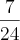

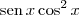 que você encontrou?
que você encontrou?
