 por pereirva » Seg Abr 20, 2009 19:12
por pereirva » Seg Abr 20, 2009 19:12
Estou com dificuldades na resolução deste exercicio
Calcule o seguinte limite, X^2- 4/x-3 em x=3
isto é "x" elevado a dois menos quatro sobre "x"-3 em que x é igual a tres.
-
pereirva
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Abr 20, 2009 19:06
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: a tentar entrar em gestao
- Andamento: cursando
 por Molina » Seg Abr 20, 2009 21:07
por Molina » Seg Abr 20, 2009 21:07
Boa noite, pereirva.
Confirme se é esse que o enunciado diz:
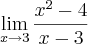
Parece ter algo estranho aí.
Veja se ao invés do 4 do numerador nao é 9 ou ao invés do 3 do denominador não é 2.
Tente utilizar o Editor de Fórmulas para escrever os limites:
equationeditorAguardo sua resposta para dar continuidade a questão.
Abraços!

Editado pela última vez por
Molina em Seg Abr 20, 2009 22:02, em um total de 1 vez.
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por marciommuniz » Seg Abr 20, 2009 21:45
por marciommuniz » Seg Abr 20, 2009 21:45
Tentei de todos os modos mas não encontro, não tem algum número errado ai não?
"Nunca penso no futuro, ele chega rápido demais." Albert Einsten
-
marciommuniz
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Abr 08, 2009 20:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Metalúrgica UFF /Química Lic. UENF
- Andamento: cursando
 por Marcampucio » Seg Abr 20, 2009 23:36
por Marcampucio » Seg Abr 20, 2009 23:36
Acho que não há nada errado.

limite pela direita
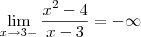
limite pela esquerda
logo não existe

o gráfico confirma:

A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por pereirva » Ter Abr 21, 2009 14:19
por pereirva » Ter Abr 21, 2009 14:19
Obrigado na resolução de exercicio nao me estava a recordar dos limites laterais. o enunciado está correcto.
No futuro vou tentar utilizar o editor de formlas thx
-
pereirva
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Abr 20, 2009 19:06
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: a tentar entrar em gestao
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [exercico UFF] Ajuda
por phmarssal » Qua Jan 14, 2015 15:13
- 2 Respostas
- 961 Exibições
- Última mensagem por DanielFerreira

Qui Jan 22, 2015 18:54
Funções
-
- Dúvida numa exercíco
por carlota_almada » Dom Dez 04, 2016 13:17
- 1 Respostas
- 2346 Exibições
- Última mensagem por Cleyson007

Seg Dez 05, 2016 20:35
Polinômios
-
- Resolução de limites
por Ana Saldanha » Sáb Mai 24, 2014 16:39
- 1 Respostas
- 1055 Exibições
- Última mensagem por e8group

Sáb Mai 24, 2014 17:44
Cálculo: Limites, Derivadas e Integrais
-
- [limites] reciso de ajuda nessa questão de limites raiz quad
por alexia » Ter Nov 15, 2011 19:55
- 1 Respostas
- 5406 Exibições
- Última mensagem por LuizAquino

Qua Nov 16, 2011 15:16
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITES] Conferir resolução
por dehcalegari » Ter Abr 16, 2013 15:19
- 4 Respostas
- 1631 Exibições
- Última mensagem por DanielFerreira

Ter Abr 16, 2013 16:39
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



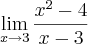



 limite pela direita
limite pela direita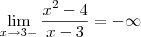 limite pela esquerda
limite pela esquerda



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.