Calcule as derivadas parciais de primeira ordem e explicite o domínio de cada função (descreva a propriedade algébrica que o define) e desenhe-o.

Eu não entendi o que o exercício quis dizer com "descreva a propriedade algébrica que o define". Seria dizer que, por exemplo, para uma a função f(x,y) =

, x + y

0.
É por aí. Para a função no seu exemplo, a propriedade algébrica que define o seu domínio seria algo do tipo:
x e
y números reais tais que

.
Ainda nesse exemplo, o esboço desse domínio seria todo o plano cartesiano retirando-se a reta

.
-civil- escreveu:Voltando à função, para esboçar o domínio, eu preciso que
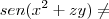
0 e deveria desenhar no gráfico

0 para mostrar que aquilo não pertence ao domínio. Mas não faço ideia de como desenhar.
Bem, primeiro note que o exercício pede que seja explicitado o domínio das funções derivadas parciais de primeira ordem. Acontece que nesse caso esse domínio será o mesmo para todas essas funções.
No caso do exercício, temos que a função k depende das variáveis x, y e z. Você precisa então calcular as derivadas parciais de primeira ordem em relação a cada uma delas.
Por exemplo, calculando a derivada parcial de k em relação a x, temos que:
![k_x = \frac{\cos z \,\textrm{sen}\,\left(x^2 + zy\right) -2x^2\cos z \cos \left(x^2 + zy\right)}{\left[\textrm{sen}\,\left(x^2 + zy\right)\right]^2} k_x = \frac{\cos z \,\textrm{sen}\,\left(x^2 + zy\right) -2x^2\cos z \cos \left(x^2 + zy\right)}{\left[\textrm{sen}\,\left(x^2 + zy\right)\right]^2}](/latexrender/pictures/e713f8139bb846f89cc89aebd9ce24a8.png)
A propriedade algébrica que define o domínio de

seria algo como:
x,
y e
z números reais tais que

.
Dos conhecimentos de trigonometria, sabemos que a função seno é igual a zero nos ângulos

, com

.
Desse modo, podemos reescrever a propriedade algébrica anterior como sendo algo do tipo:
x,
y e
z números reais tais que

, com

.
Um esboço desse domínio seria todo o espaço
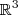
retirando-se as superfícies
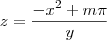
(quando
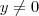
) e retirando-se as retas
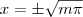
que estão sobre o plano xOz (quando

e

).
Para fazer o esboço das superfícies, note que as curvas de nível de cada um deles são parábolas.

 , x + y
, x + y  0 ?
0 ?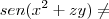 0 e deveria desenhar no gráfico
0 e deveria desenhar no gráfico  0 para mostrar que aquilo não pertence ao domínio. Mas não faço ideia de como desenhar.
0 para mostrar que aquilo não pertence ao domínio. Mas não faço ideia de como desenhar.


 .
. .
.![k_x = \frac{\cos z \,\textrm{sen}\,\left(x^2 + zy\right) -2x^2\cos z \cos \left(x^2 + zy\right)}{\left[\textrm{sen}\,\left(x^2 + zy\right)\right]^2} k_x = \frac{\cos z \,\textrm{sen}\,\left(x^2 + zy\right) -2x^2\cos z \cos \left(x^2 + zy\right)}{\left[\textrm{sen}\,\left(x^2 + zy\right)\right]^2}](/latexrender/pictures/e713f8139bb846f89cc89aebd9ce24a8.png)
 seria algo como:
seria algo como:  .
. , com
, com  .
. , com
, com 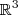 retirando-se as superfícies
retirando-se as superfícies 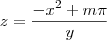 (quando
(quando 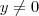 ) e retirando-se as retas
) e retirando-se as retas 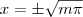 que estão sobre o plano xOz (quando
que estão sobre o plano xOz (quando  e
e  ).
).


 , avisa que eu resolvo.
, avisa que eu resolvo.

