Talvez eu esteja esquecendo algum detalhe muito idiota, mas o fato é que não estou conseguindo compreender um passo da resolução da seguinte questão:
Prove, pela definição formal de limite, que
Então tudo a fazer é achar
 e
e  tal que
tal que![9-\delta<x<9 \rightarrow \left| \sqrt[4]{9-x} \right|<\epsilon 9-\delta<x<9 \rightarrow \left| \sqrt[4]{9-x} \right|<\epsilon](/latexrender/pictures/e8585e9762d1f9833027f3505a75cce8.png)
Desenvolvendo o lado direito...
Mas neste passo eu páro.
De algum modo, segundo a resolução mostrada no livro, é lícito saltar daí para:
Como? Não entendo esse passo. Inverter
 e
e  , tudo bem. Mas não entendo o que garante que
, tudo bem. Mas não entendo o que garante que 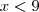 . Até onde vejo, é perfeitamente possível que
. Até onde vejo, é perfeitamente possível que  , mas que
, mas que  . No entanto esse passo é necessário para concluir o exercício e provar o limite (o resto eu sei).
. No entanto esse passo é necessário para concluir o exercício e provar o limite (o resto eu sei).Obrigado pela atenção.

![\lim_{x\rightarrow{9}^{-}} \sqrt[4]{9-x} = 0 \lim_{x\rightarrow{9}^{-}} \sqrt[4]{9-x} = 0](/latexrender/pictures/b8be27c8006f5df87b787b6620ca4066.png)
![\left| \sqrt[4]{9-x} \right|<\epsilon \left| \sqrt[4]{9-x} \right|<\epsilon](/latexrender/pictures/03a5094edc5ec894de27daff09d59501.png)
![\sqrt[4]{9-x}<\epsilon \sqrt[4]{9-x}<\epsilon](/latexrender/pictures/cd0eeb6724997eb3d2178a17b67798cc.png)



 ) . Dessa forma,
) . Dessa forma, 

 .
.
 :
: