 por carvalhothg » Qua Set 28, 2011 15:32
por carvalhothg » Qua Set 28, 2011 15:32
Seja
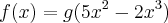
uma função derivável. Se f''(2) = -122 e g'(4) = 3. Então quanto vale g''(4)?
Pessoal, como resolvo este exercício estou me enrolando todo. Eu tentei resolver e encontrei
f''(2)=g''(4) que é igual a -122. Mas acredito que eu esteja errado, vcs poderia me dar uma força?
-
carvalhothg
- Usuário Dedicado

-
- Mensagens: 42
- Registrado em: Dom Set 04, 2011 18:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por LuizAquino » Qua Set 28, 2011 17:42
por LuizAquino » Qua Set 28, 2011 17:42
carvalhothg escreveu:Seja
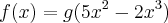
uma função derivável. Se f''(2) = -122 e g'(4) = 3. Então quanto vale g''(4)?
Aplicando a regra da cadeia, temos que:
![f^\prime(x)=\left[g\left(5{x}^{2}-2{x}^{3}\right)\right]^\prime \Rightarrow f^\prime(x)= g^\prime\left(5{x}^{2}-2{x}^{3}\right)\left(10x - 6x^2\right) f^\prime(x)=\left[g\left(5{x}^{2}-2{x}^{3}\right)\right]^\prime \Rightarrow f^\prime(x)= g^\prime\left(5{x}^{2}-2{x}^{3}\right)\left(10x - 6x^2\right)](/latexrender/pictures/baa0517c0995ddd3ab9710cad4ff6a75.png)
Aplicando a regra do produto e a regra da cadeia, temos que:
![f^{\prime\prime}(x)= \left[g^\prime\left(5{x}^{2}-2{x}^{3}\right)\left(10x - 6x^2\right)\right]^\prime f^{\prime\prime}(x)= \left[g^\prime\left(5{x}^{2}-2{x}^{3}\right)\left(10x - 6x^2\right)\right]^\prime](/latexrender/pictures/2468e4c05d9ba9cefbc245752f3720d9.png)
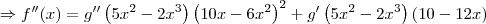
Agora tente terminar o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 12550 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
-
- [derivada] derivada pela definição da secante
por TheKyabu » Sáb Out 27, 2012 23:24
- 2 Respostas
- 10878 Exibições
- Última mensagem por TheKyabu

Dom Out 28, 2012 11:44
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Com duas variáveis e derivada mista
por leticiaeverson » Dom Abr 22, 2018 00:39
- 3 Respostas
- 13186 Exibições
- Última mensagem por Gebe

Dom Abr 22, 2018 17:11
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada]derivada de função de raiz cúbica
por armando » Sáb Jul 20, 2013 15:22
- 4 Respostas
- 14791 Exibições
- Última mensagem por armando

Dom Jul 21, 2013 22:17
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADA] DERIVADA POR DEFINIÇÃO DA RAIZ DO MÓDULO DE X
por Matheusgdp » Qua Set 16, 2015 04:07
- 2 Respostas
- 5106 Exibições
- Última mensagem por Matheusgdp

Qui Set 17, 2015 18:31
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
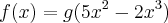 uma função derivável. Se f''(2) = -122 e g'(4) = 3. Então quanto vale g''(4)?
uma função derivável. Se f''(2) = -122 e g'(4) = 3. Então quanto vale g''(4)?

![f^\prime(x)=\left[g\left(5{x}^{2}-2{x}^{3}\right)\right]^\prime \Rightarrow f^\prime(x)= g^\prime\left(5{x}^{2}-2{x}^{3}\right)\left(10x - 6x^2\right) f^\prime(x)=\left[g\left(5{x}^{2}-2{x}^{3}\right)\right]^\prime \Rightarrow f^\prime(x)= g^\prime\left(5{x}^{2}-2{x}^{3}\right)\left(10x - 6x^2\right)](/latexrender/pictures/baa0517c0995ddd3ab9710cad4ff6a75.png)
![f^{\prime\prime}(x)= \left[g^\prime\left(5{x}^{2}-2{x}^{3}\right)\left(10x - 6x^2\right)\right]^\prime f^{\prime\prime}(x)= \left[g^\prime\left(5{x}^{2}-2{x}^{3}\right)\left(10x - 6x^2\right)\right]^\prime](/latexrender/pictures/2468e4c05d9ba9cefbc245752f3720d9.png)
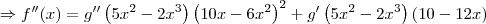

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
