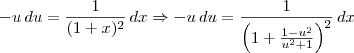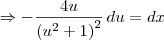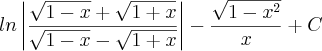por rubenesantos » Dom Set 25, 2011 18:35
por rubenesantos » Dom Set 25, 2011 18:35
Olá pessoal, boa tarde.
Estou com uma Integral de função irracional e não estou sabendo como proceder. Substituição, partes, trinômio, racionais... Já fiz várias dessas questões, mas parece que algumas de funções irracionais são bem chatinhas. Ainda estou tendo dificuldade... Tirando essa dúvida, acredito que poderei responder as demais, pois são parecidas com ela.
Aqui está a bendita:

Já tentei chamar toda a raíz de "t", mas quando faço isso tenho problemas com o

. Daí não consigo achar o x.
Se alguém puder ajudar, ficarei muito grato.
Abraços.
-
rubenesantos
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Seg Mai 02, 2011 22:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por rubenesantos » Seg Set 26, 2011 02:05
por rubenesantos » Seg Set 26, 2011 02:05
Beleza mano... acabou sendo uma substituição simples (apesar de trabalhosa). Quando chamava toda a raíz de "u" tinha problema para isolar o x, mas depois da explicação fiquei certo que é possível. Agora fiquei com um polinômio de grau 2 no numerador e outro de grau 4 no denominador que dá pra simplificar usando o conceito de equação biquadrada.
Usei e achei as raízes: u1 = 1, u2 = -1, u3 = 1, u4 = -1.
Agora vou trabalhar em cima dessa racional que me apareceu. Definitivamente essa é uma integral bastante trabalhosa.
Muito obrigado pela ajuda. Quando terminar de respondê-la volto aqui pra agradecer mais uma vez! =D
-
rubenesantos
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Seg Mai 02, 2011 22:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por rubenesantos » Ter Set 27, 2011 00:16
por rubenesantos » Ter Set 27, 2011 00:16
Com a ajuda do colega Luíz Aquino, consegui chegar até aqui:

A partir daí chego num resultado que acredito que é satisfatório. Mas, queria saber como faço pra chegar no resultado da lista, acredito que é uma integral imediata... Não consegui chegar de jeito nenhum nela. Essa é a resposta que me aparece na lista de exercícios:
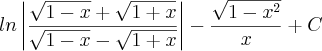
Desde já agradeço a ajuda.
-
rubenesantos
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Seg Mai 02, 2011 22:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Ter Set 27, 2011 08:07
por LuizAquino » Ter Set 27, 2011 08:07
rubenesantos escreveu:A partir daí chego num resultado que acredito que é satisfatório. Mas, queria saber como faço pra chegar no resultado da lista, acredito que é uma integral imediata...
Qual foi o resultado que você chegou? Provavelmente a sua dificuldade está em aplicar propriedades dos logaritmos. Vale a pena você revisar esse conteúdo. Se desejar, assista a sequência de
vídeo-aulas "Matemática - Aula 13 - Logaritmo" (Parte de 1 até 4) do Nerckie.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por rubenesantos » Sex Set 30, 2011 10:34
por rubenesantos » Sex Set 30, 2011 10:34
Consegui mano! Vc é o cara.
Depois de muitas operações com as frações, consegui chegar exatamente ao resultado da lista. =D
Muito obrigado pela ajuda! =D
-
rubenesantos
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Seg Mai 02, 2011 22:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral função irracional
por manuel_pato1 » Dom Jan 20, 2013 14:16
- 2 Respostas
- 2629 Exibições
- Última mensagem por manuel_pato1

Dom Jan 20, 2013 21:08
Cálculo: Limites, Derivadas e Integrais
-
- Integral de função com expoente irracional
por carlos_araujo » Sex Dez 05, 2014 16:54
- 1 Respostas
- 2047 Exibições
- Última mensagem por adauto martins

Qua Dez 10, 2014 15:27
Cálculo: Limites, Derivadas e Integrais
-
- Definição de função racional e irracional
por Soprano » Sex Set 30, 2016 19:52
- 0 Respostas
- 2603 Exibições
- Última mensagem por Soprano

Sex Set 30, 2016 19:52
Funções
-
- [Dúvida]Função Trigonométrica Inversa em Integral.
por Jhonata » Qui Jun 07, 2012 18:06
- 2 Respostas
- 1941 Exibições
- Última mensagem por Jhonata

Qui Jun 07, 2012 20:40
Cálculo: Limites, Derivadas e Integrais
-
- [Dúvida] Integral e ponto máximo de uma função
por ruisu » Seg Mar 04, 2013 15:19
- 1 Respostas
- 1577 Exibições
- Última mensagem por young_jedi

Seg Mar 04, 2013 23:14
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

 . Daí não consigo achar o x.
. Daí não consigo achar o x.



![du = \frac{1}{2\sqrt{\frac{1-x}{1+x}}}\left[\frac{-2}{(1+x)^2}\right] \, dx \Rightarrow -u\,du = \frac{1}{(1+x)^2}\,dx du = \frac{1}{2\sqrt{\frac{1-x}{1+x}}}\left[\frac{-2}{(1+x)^2}\right] \, dx \Rightarrow -u\,du = \frac{1}{(1+x)^2}\,dx](/latexrender/pictures/6ef934f15499da0193f70eb7424b3714.png)
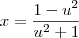 . Desse modo, temos que:
. Desse modo, temos que: