Como calcular a área da região limitada pelo gráfico da função y = x elevado a 3 e pela reta y = 3x - 2 , que é tangente à curva y = x elevado a 3 no ponto (1,1).
Obs: Encontrei onde as funções se interceptam(pontos -2 e 1), mas estou com dúvidas na conclusão do exercício pois achei o resultado 11/4 u.a. mas ao conferir a resposta encontrei o resultado 27/4 u.a. Gostaria de saber onde errei.
Grato desde já.
está acima da reta 
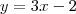no intervalo [-2, 1]. Isto é, temos que 
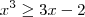para valores de x no intervalo [-2, 1].![\int_{-2}^1 x^3 - (3x-2)\,dx = \left[\frac{x^4}{4} - \frac{3x^2}{2} + 2x\right]_{-2}^1](/latexrender/pictures/911e89bd9e33df9f97c7957ea57bea95.png "\int_{-2}^1 x^3 - (3x-2)\,dx = \left[\frac{x^4}{4} - \frac{3x^2}{2} + 2x\right]_{-2}^1")
![= \left(\frac{1^4}{4} - \frac{3\cdot 1^2}{2} + 2\cdot 1\right) - \left[\frac{(-2)^4}{4} - \frac{3\cdot (-2)^2}{2} + 2\cdot (-2)\right] = \frac{27}{4}](/latexrender/pictures/22fac1b71c0b5d5e2a5d72c74c184808.png "= \left(\frac{1^4}{4} - \frac{3\cdot 1^2}{2} + 2\cdot 1\right) - \left[\frac{(-2)^4}{4} - \frac{3\cdot (-2)^2}{2} + 2\cdot (-2)\right] = \frac{27}{4}")
por 
.
: