 por caiofisico » Seg Set 05, 2011 20:18
por caiofisico » Seg Set 05, 2011 20:18
pessoal gostaria de saber se estou no caminho ou se errei em algum dado momento
Ache a derivada de

então fiz o seguinte...



bom resolvendo isso achei que 2/2= 1
achei estranho pois na copia que fiz de um caderno estava assim:
.......
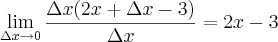
do modo que eu fiz esta errado? usei a formula errada? acredito que seja essa formula mesmo
-
caiofisico
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Sáb Ago 20, 2011 22:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por LuizAquino » Seg Set 05, 2011 21:56
por LuizAquino » Seg Set 05, 2011 21:56
caiofisico escreveu:Ache a derivada de

então fiz o seguinte...


Você errou no cálculo da função. Veja que:
![\lim_{\Delta x \rightarrow 0} \frac{f(x+\Delta x) - f(x)}{\Delta x} =\lim_{\Delta x \to 0} \frac{[\left(x+\Delta x\right)^2 - 3(x+\Delta x)] - (x^2 - 3x)}{\Delta x} \lim_{\Delta x \rightarrow 0} \frac{f(x+\Delta x) - f(x)}{\Delta x} =\lim_{\Delta x \to 0} \frac{[\left(x+\Delta x\right)^2 - 3(x+\Delta x)] - (x^2 - 3x)}{\Delta x}](/latexrender/pictures/3f5d75cba62e2dbcc6a30189ceae2fde.png)
Agora tente terminar o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por caiofisico » Seg Set 05, 2011 22:09
por caiofisico » Seg Set 05, 2011 22:09
opa já tinha conseguido

muito obrigado, entendi agora o porque de estar ao quadrado e o outro sendo multiplicado por 3, era simplesmente olhar a equação ^^, falta de atenção a minha, obrigado amigo
-
caiofisico
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Sáb Ago 20, 2011 22:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por LuizAquino » Seg Set 05, 2011 22:57
por LuizAquino » Seg Set 05, 2011 22:57
caiofisico escreveu:muito obrigado, entendi agora o porque de estar ao quadrado e o outro sendo multiplicado por 3, era simplesmente olhar a equação ^^, falta de atenção a minha, obrigado amigo
Apenas lembrando: você precisou olhar para uma
função e não para uma
equação como você disse.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por caiofisico » Ter Set 06, 2011 19:44
por caiofisico » Ter Set 06, 2011 19:44
^^ isso isso, ainda to acostumando com a linguagem

-
caiofisico
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Sáb Ago 20, 2011 22:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivada: Achar os extremos da função(min/máx/inflexão)
por Fernandobertolaccini » Dom Jul 13, 2014 22:50
- 1 Respostas
- 1785 Exibições
- Última mensagem por e8group

Seg Jul 14, 2014 01:48
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] ajuda para achar quais pontos a função é diferenc
por leohapo » Seg Nov 21, 2016 17:46
- 1 Respostas
- 7506 Exibições
- Última mensagem por adauto martins

Sáb Dez 10, 2016 11:18
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 12556 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
-
- Achar derivada
por Kathleen » Dom Jun 26, 2011 19:20
- 5 Respostas
- 2910 Exibições
- Última mensagem por Neperiano

Dom Jun 26, 2011 21:59
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada]derivada de função de raiz cúbica
por armando » Sáb Jul 20, 2013 15:22
- 4 Respostas
- 14795 Exibições
- Última mensagem por armando

Dom Jul 21, 2013 22:17
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




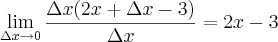





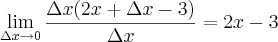

![\lim_{\Delta x \rightarrow 0} \frac{f(x+\Delta x) - f(x)}{\Delta x} =\lim_{\Delta x \to 0} \frac{[\left(x+\Delta x\right)^2 - 3(x+\Delta x)] - (x^2 - 3x)}{\Delta x} \lim_{\Delta x \rightarrow 0} \frac{f(x+\Delta x) - f(x)}{\Delta x} =\lim_{\Delta x \to 0} \frac{[\left(x+\Delta x\right)^2 - 3(x+\Delta x)] - (x^2 - 3x)}{\Delta x}](/latexrender/pictures/3f5d75cba62e2dbcc6a30189ceae2fde.png)





