 por vmouc » Qui Set 01, 2011 18:03
por vmouc » Qui Set 01, 2011 18:03
Boa tarde,
Prezados colega,
Gostaria de contar com a colaboração de vocês para entender o processo de resolução da seguinte integral definida:

Eu sei que os intervalos estão de uma forma não convencional mas é assim que está no exercício do livro. Fiz diversas tentativas mas não consegui alcançar o resultado
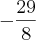
, o qual me foi passado pelo professor.
Alguem poderia, por gentileza, me informar passo a passo o processo de resolução deste tipo de integral definida?
Atenciosamente,
Vinícius
Vinícius Costa
-
vmouc
- Usuário Dedicado

-
- Mensagens: 43
- Registrado em: Sáb Mar 05, 2011 22:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
-
 por LuizAquino » Qui Set 01, 2011 18:05
por LuizAquino » Qui Set 01, 2011 18:05
DicaNote que:
 Observação
Observaçãovmouc escreveu:Eu sei que os intervalos estão de uma forma não convencional mas é assim que está no exercício do livro.
"
Não convencional"? Não há problema algum com o intervalo de integração apresentado.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por vmouc » Qui Set 01, 2011 18:19
por vmouc » Qui Set 01, 2011 18:19
Geralmente o intervalo superior é o numero maior e o inferior é o numero menor, pelo que eu havia entendido. Está certo?
Vinícius Costa
-
vmouc
- Usuário Dedicado

-
- Mensagens: 43
- Registrado em: Sáb Mar 05, 2011 22:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
-
 por vmouc » Qui Set 01, 2011 18:28
por vmouc » Qui Set 01, 2011 18:28
Pois é, minha resolução ficou:

![2[-{t}^{-1}]-7[-\frac{{t}^{-2}}{2}] 2[-{t}^{-1}]-7[-\frac{{t}^{-2}}{2}]](/latexrender/pictures/f0f43fde1b83aad7c1198ccdc7ae1082.png)
Mas ao substituir não dá certo
Vinícius Costa
-
vmouc
- Usuário Dedicado

-
- Mensagens: 43
- Registrado em: Sáb Mar 05, 2011 22:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
-
 por LuizAquino » Qui Set 01, 2011 18:54
por LuizAquino » Qui Set 01, 2011 18:54
vmouc escreveu:Geralmente o intervalo superior é o numero maior e o inferior é o numero menor, pelo que eu havia entendido. Está certo?
Não há problema quanto a isso. Basta lembrar da propriedade:

.
vmouc escreveu:Pois é, minha resolução ficou:

![2[-{t}^{-1}]-7[-\frac{{t}^{-2}}{2}] 2[-{t}^{-1}]-7[-\frac{{t}^{-2}}{2}]](/latexrender/pictures/f0f43fde1b83aad7c1198ccdc7ae1082.png)
Mas ao substituir não dá certo
Você deve estar se atrapalhando nas substituições. Envie o procedimento que você fez depois desse ponto.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Resolução de Integral Definida]
por Seza Saenz » Qui Mar 24, 2016 15:18
- 0 Respostas
- 2000 Exibições
- Última mensagem por Seza Saenz

Qui Mar 24, 2016 15:18
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL DEFINIDA] Duvidas na resolução
por fabriel » Sex Mar 22, 2013 13:09
- 1 Respostas
- 1425 Exibições
- Última mensagem por young_jedi

Sáb Mar 23, 2013 16:42
Cálculo: Limites, Derivadas e Integrais
-
- [Integral Definida] Está certa minha resolução?
por Fabio Wanderley » Seg Out 22, 2012 23:37
- 2 Respostas
- 2032 Exibições
- Última mensagem por Fabio Wanderley

Ter Out 23, 2012 00:45
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Resolver Integral definida com trigonometria
por rodrigoboreli » Dom Set 07, 2014 01:02
- 1 Respostas
- 4342 Exibições
- Última mensagem por adauto martins

Sex Out 17, 2014 12:39
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo Integral] Integral Definida
por ARCS » Sáb Fev 02, 2013 21:37
- 2 Respostas
- 3671 Exibições
- Última mensagem por e8group

Sáb Fev 02, 2013 22:13
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

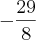 , o qual me foi passado pelo professor.
, o qual me foi passado pelo professor.




![2[-{t}^{-1}]-7[-\frac{{t}^{-2}}{2}] 2[-{t}^{-1}]-7[-\frac{{t}^{-2}}{2}]](/latexrender/pictures/f0f43fde1b83aad7c1198ccdc7ae1082.png)
 .
.
 .
.
 :
: