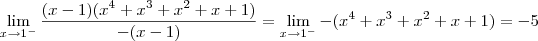por killerkill » Sáb Ago 20, 2011 13:18
por killerkill » Sáb Ago 20, 2011 13:18
Sou eu mais uma vez!
O exercício dessa vez é um limite de uma função modular.
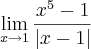
se x>1
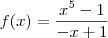
se x<1
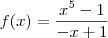
Então analisando os limites laterais:
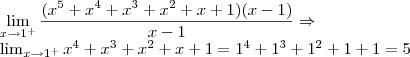
e
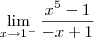
não sei oque faço agora com esse limite . Não sei como eliminar a indeterminação dele.
-
killerkill
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Ter Ago 09, 2011 22:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eg. Elétrica
- Andamento: cursando
 por MarceloFantini » Sáb Ago 20, 2011 14:49
por MarceloFantini » Sáb Ago 20, 2011 14:49
Note que
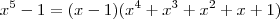
, logo:
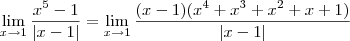
. Tente analisar o sinal agora.
Cuidado:
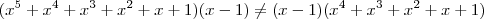
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por killerkill » Sáb Ago 20, 2011 17:05
por killerkill » Sáb Ago 20, 2011 17:05
Marcelo, confesso que estou meio perdido quanto ao conceito de módulo nesse exercício... a unica coisa que sei é o seguinte..
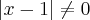
até onde eu sabia esse módulo poderia ser duas coisas.. ou x-1 ou -x+1... realmente estou perdendo algum detalhe do fundamento, sou meio fraco nisso... me ajuda por favor? oque eu devo fazer com o módulo? ele nao assume x-1 em uma possibilidade e -x+1 em outra nao? poderia me explicar por favor?
-
killerkill
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Ter Ago 09, 2011 22:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eg. Elétrica
- Andamento: cursando
 por LuizAquino » Seg Ago 22, 2011 09:00
por LuizAquino » Seg Ago 22, 2011 09:00
killerkill escreveu:o que eu devo fazer com o módulo?
Como o colega Fantini disse, temos que
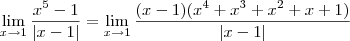
Aplicando a definição de módulo, os limites laterais ficam como:
(i)
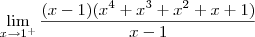
;
(ii)
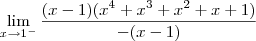
.
Agora termine o exercício.
ObservaçãoSe
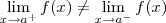
, então dizemos que

não existe.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por killerkill » Seg Ago 22, 2011 10:15
por killerkill » Seg Ago 22, 2011 10:15
Luiz, foi isso que eu fiz, inclusive minha dúvida inicial é essa, pois não consegui determinar o limite quando x tende a 1 um por valores menores que ele. Então no caso meu raciocínio estava correto, ja que analisei os limites laterais. só não consegui resolver esse limite lateral.
-
killerkill
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Ter Ago 09, 2011 22:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eg. Elétrica
- Andamento: cursando
 por LuizAquino » Seg Ago 22, 2011 10:52
por LuizAquino » Seg Ago 22, 2011 10:52
killerkill escreveu:Luiz, foi isso que eu fiz, inclusive minha dúvida inicial é essa, pois não consegui determinar o limite quando x tende a 1 um por valores menores que ele.
Note que:
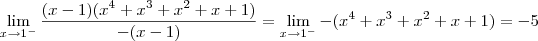
killerkill escreveu:Então no caso meu raciocínio estava correto, ja que analisei os limites laterais. só não consegui resolver esse limite lateral.
De fato, você estava no caminho. Mas, vale lembrar que, como o Fantini apontou acima, você errou o produto notável no numerador.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por killerkill » Seg Ago 22, 2011 12:32
por killerkill » Seg Ago 22, 2011 12:32
Eu notei o erro depois, mais foi erro na hora do editor de formulas, ctrl c e ctrl v, hehe... pode deixar que as regrinhas de fatoração estou por dentro.. =D mais quanto a questão, putz! é verdade, eu estava colocando o (-) no x e o (+) no 1, e depois não sabia como cancelava o denominador com o termo do numerador. mais agora vi oque eu estava fazendo errado, bastava cancelar o termo e depois o menos faria o polinômio ficar negativo. Luiz e Marcelo, muito obrigado!
-
killerkill
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Ter Ago 09, 2011 22:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eg. Elétrica
- Andamento: cursando
 por LuizAquino » Seg Ago 22, 2011 12:44
por LuizAquino » Seg Ago 22, 2011 12:44
killerkill escreveu:putz! é verdade, eu estava colocando o (-) no x e o (+) no 1, e depois não sabia como cancelava o denominador com o termo do numerador.
Veja o tópico:
Dúvida simples sobre algebra.viewtopic.php?f=106&t=5466
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por killerkill » Dom Set 04, 2011 16:45
por killerkill » Dom Set 04, 2011 16:45
esse limite nao existe então ne? ja que os limites laterais sao diferentes.
-
killerkill
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Ter Ago 09, 2011 22:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eg. Elétrica
- Andamento: cursando
 por LuizAquino » Dom Set 04, 2011 17:18
por LuizAquino » Dom Set 04, 2011 17:18
killerkill escreveu:esse limite nao existe então ne? ja que os limites laterais sao diferentes.
De fato ele não existe.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limite modular, me ajudem!
por arthurvct » Ter Abr 23, 2013 14:50
- 3 Respostas
- 1526 Exibições
- Última mensagem por arthurvct

Ter Abr 23, 2013 17:18
Cálculo: Limites, Derivadas e Integrais
-
- Funçao modular
por Fiel8 » Sex Jul 10, 2009 19:25
- 1 Respostas
- 2616 Exibições
- Última mensagem por Molina

Sex Jul 10, 2009 21:50
Funções
-
- Função Modular
 por geriane » Sáb Abr 03, 2010 21:32
por geriane » Sáb Abr 03, 2010 21:32
- 3 Respostas
- 3119 Exibições
- Última mensagem por Molina

Dom Abr 04, 2010 12:57
Funções
-
- Funçao modular
 por Skcedas » Qua Mai 26, 2010 19:29
por Skcedas » Qua Mai 26, 2010 19:29
- 6 Respostas
- 5375 Exibições
- Última mensagem por netlopes

Ter Jun 08, 2010 18:11
Funções
-
- Função Modular
 por DanieldeLucena » Seg Set 20, 2010 18:03
por DanieldeLucena » Seg Set 20, 2010 18:03
- 1 Respostas
- 2245 Exibições
- Última mensagem por MarceloFantini

Seg Set 20, 2010 19:35
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
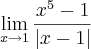
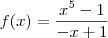
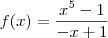
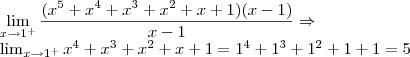
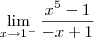

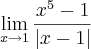
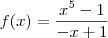
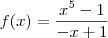
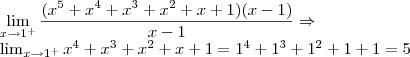
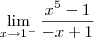

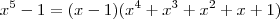 , logo:
, logo: 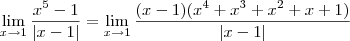 . Tente analisar o sinal agora.
. Tente analisar o sinal agora.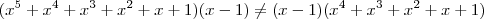 .
.

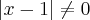

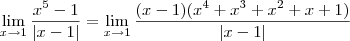
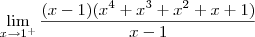 ;
;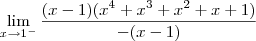 .
.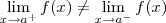 , então dizemos que
, então dizemos que  não existe.
não existe.