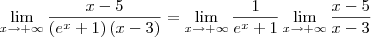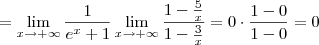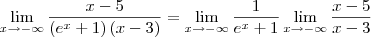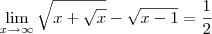por killerkill » Qui Ago 18, 2011 00:30
por killerkill » Qui Ago 18, 2011 00:30
Calcule o limite:
Só consegui fazer assim:
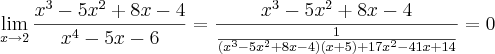
não sei se a ideia da manipulaçao algébrica esta correta... no caso fazer a divisao do denominador pelo numerador atraves do método da chave encontrando uma resposta e colocando ela como denominador e no numerador 1. ou seja, seria a resposta da primeira divisao elevada a -1 ja que o expoente do denominador é de 1 grau menor que o do numerador.
nao tenho gabarito para corrigir.
Outra questao que nao consigo é:
![\lim_{x\rightarrow\infty}\sqrt[2]{x+\sqrt[2]{x}}-\sqrt[2]{x-1} \lim_{x\rightarrow\infty}\sqrt[2]{x+\sqrt[2]{x}}-\sqrt[2]{x-1}](/latexrender/pictures/190833bac7797bdc3143e90e07c91104.png)
O estranho é que o professor não nos ensinou aquele método que vocês costumam usar aqui no fórum que é de substituir determinado termo por uma outra letra etc. Não sei nem dizer se isso é pra ser estudado agora ou só mais tarde. Alguém me ajuda?
-
killerkill
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Ter Ago 09, 2011 22:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eg. Elétrica
- Andamento: cursando
 por LuizAquino » Qui Ago 18, 2011 07:53
por LuizAquino » Qui Ago 18, 2011 07:53
killerkill escreveu: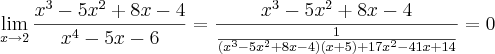
Errado! Note que se você desenvolver o que está no segundo membro, você
não obtém o que está no primeiro:
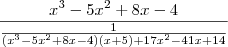
![= (x^3-5x^2+8x-4) \cdot \left[\frac{(x^3-5x^2+8x-4)(x+5)+17x^2-41x+14}{1}\right] = (x^3-5x^2+8x-4) \cdot \left[\frac{(x^3-5x^2+8x-4)(x+5)+17x^2-41x+14}{1}\right]](/latexrender/pictures/e942348fc8df8f63916cb606c2e4cf3f.png)

Além disso, novamente você
não está colocando a notação de limite em cada passo.
Para resolver exercícios como esse é necessário efetuar a fatoração dos polinômios. Se você não se recorda como fazer isso, então eu recomendo que você revise esse conteúdo do ensino médio.
Realizando a fatoração você obtém:
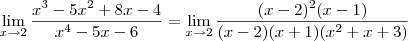
Agora termine o exercício.
killerkill escreveu: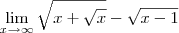
A estratégia nesse limite é dividir e multiplicar por
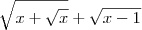
:
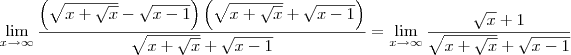
Em seguida, divida tanto o numerador quanto o denominador por

:
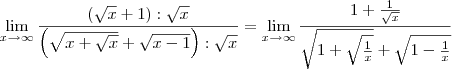
Agora termine o exercício.
killerkill escreveu:O estranho é que o professor não nos ensinou aquele método que vocês costumam usar aqui no fórum que é de substituir determinado termo por uma outra letra etc. Não sei nem dizer se isso é pra ser estudado agora ou só mais tarde.
Geralmente essas estratégias de substituição são estudadas ao longo da apresentação dos limites. Entretanto, tipicamente os livros não separam uma seção específica para exibir a técnica. Alguns professores ensinam a técnica a medida que vão exibindo como calcular limites.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por killerkill » Qui Ago 18, 2011 12:20
por killerkill » Qui Ago 18, 2011 12:20
Obrigado Luiz. só nao entendi a passagem do denominador no caso
![\frac{\sqrt[]{x}}{x}\Rightarrow \sqrt[]{\frac{1}{x}} \frac{\sqrt[]{x}}{x}\Rightarrow \sqrt[]{\frac{1}{x}}](/latexrender/pictures/f499b7d38ffc7736042e9571b020b535.png)
Aproveitando... preciso de sua ajuda aqui nessa outra questão :
Determine os pontos de continuidade e assintotas verticais e horizontais da funçao:
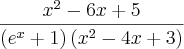
Oque eu consegui fazer foi:
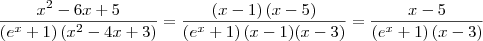
A funçao nao está definida para x=3 ou seja ela é descontínua em x=3. Para verificar se esse valor x é uma assíntota verifica-se:
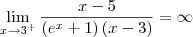
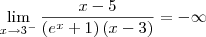
Portanto x=3 é uma assíntota vertical.
Para as assintotas horizontais fiz
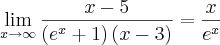
(dividi todos os termos por x
mais a partir daí nao sei mais analisar.
Ontem fiquei ate as 3:30da manha aqui tentanto resolver e nao consegui resolver nenhuma questao dessa prova antiga dele! PQP.. to perdido mesmo!!!
-
killerkill
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Ter Ago 09, 2011 22:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eg. Elétrica
- Andamento: cursando
 por LuizAquino » Qui Ago 18, 2011 21:19
por LuizAquino » Qui Ago 18, 2011 21:19
killerkill escreveu:só nao entendi a passagem do denominador no caso
![\frac{\sqrt[]{x}}{x}\Rightarrow \sqrt[]{\frac{1}{x}} \frac{\sqrt[]{x}}{x}\Rightarrow \sqrt[]{\frac{1}{x}}](/latexrender/pictures/f499b7d38ffc7736042e9571b020b535.png)
Seja
x um número real positivo não nulo. Temos que:
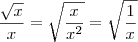
killerkill escreveu:Aproveitando... preciso de sua ajuda aqui nessa outra questão :
Determine os pontos de continuidade e assintotas verticais e horizontais da funçao:
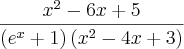
Por questão de organização, o ideal é que em cada tópico tenha apenas um exercício. Fica o lembrete para as próximas vezes.
killerkill escreveu:O que eu consegui fazer foi:
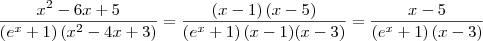
Considerando que x deve ser diferente de 1, está correto esse desenvolvimento.
Mas, lembre-se que a função original não estará definida em 1.
killerkill escreveu:A funçao nao está definida para x=3 ou seja ela é descontínua em x=3. Para verificar se esse valor x é uma assíntota verifica-se:
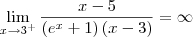
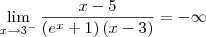
Portanto x=3 é uma assíntota vertical.
Correção:
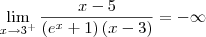
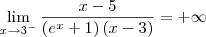
killerkill escreveu:Para as assintotas horizontais fiz
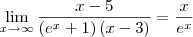
(dividi todos os termos por x
Essa operação está incorreta.
A maneira adequada é algo como:
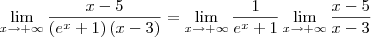
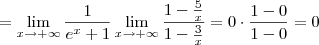
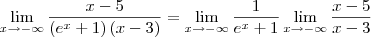

killerkill escreveu:Ontem fiquei ate as 3:30 da manha aqui tentanto resolver e nao consegui resolver nenhuma questao dessa prova antiga dele!
O importante é que você está estudando. Pior seria se você não estivesse.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por killerkill » Sex Ago 19, 2011 11:43
por killerkill » Sex Ago 19, 2011 11:43
Beleza! a minha resposta deu 1/2
=D acho que está certo. obrigado pela ajuda novamente!
-
killerkill
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Ter Ago 09, 2011 22:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eg. Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6646 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4792 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5121 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7263 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções piso (maior inteiro)
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
- 2 Respostas
- 4440 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
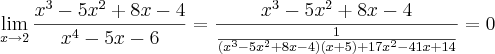
![\lim_{x\rightarrow\infty}\sqrt[2]{x+\sqrt[2]{x}}-\sqrt[2]{x-1} \lim_{x\rightarrow\infty}\sqrt[2]{x+\sqrt[2]{x}}-\sqrt[2]{x-1}](/latexrender/pictures/190833bac7797bdc3143e90e07c91104.png)


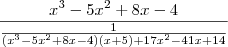
![= (x^3-5x^2+8x-4) \cdot \left[\frac{(x^3-5x^2+8x-4)(x+5)+17x^2-41x+14}{1}\right] = (x^3-5x^2+8x-4) \cdot \left[\frac{(x^3-5x^2+8x-4)(x+5)+17x^2-41x+14}{1}\right]](/latexrender/pictures/e942348fc8df8f63916cb606c2e4cf3f.png)

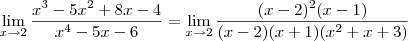
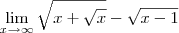
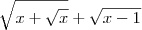 :
: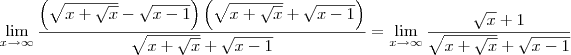
 :
: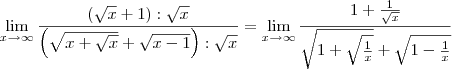

![\frac{\sqrt[]{x}}{x}\Rightarrow \sqrt[]{\frac{1}{x}} \frac{\sqrt[]{x}}{x}\Rightarrow \sqrt[]{\frac{1}{x}}](/latexrender/pictures/f499b7d38ffc7736042e9571b020b535.png)
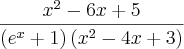
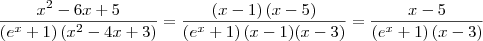
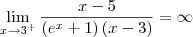
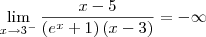
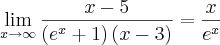 (dividi todos os termos por x
(dividi todos os termos por x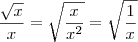
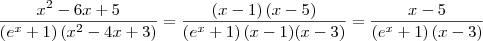
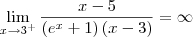
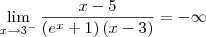
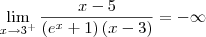
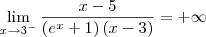
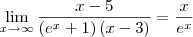 (dividi todos os termos por x
(dividi todos os termos por x