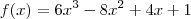Caroline Oliveyra escreveu:Se alguém sabe como resolver isso por derivada por favor me ajude!!
Mesmo que até o momento você só tenha estudado o conceito de derivada, você pode responder a seguinte pergunta:
Qual é o polinômio
F(
x) que ao ser derivado resulta em
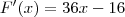
?
Ora, do conhecimento sobre derivada de polinômios você deve concluir que
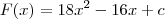
, sendo
c uma constante.
Desse modo, da informação 2), como
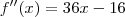
, temos que

.
Por outro lado, sabemos que a reta tangente ao gráfico de f no ponto (1, 3) deve ser

. Mas, da informação 1) temos que essa reta é
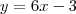
. Comparando essas duas equações, obtemos que

.
Voltando a

, se calculamos
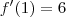
ficamos com a equação:

Disso obtemos que

. Isso significa que
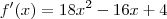
.
Agora, responda a pergunta:
Qual é o polinômio
f(
x) que ao ser derivado resulta em
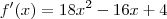
?
Ora, do conhecimento sobre derivada de polinômios você deve concluir que
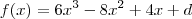
, sendo
d uma constante.
Ainda da informação 1), sabemos que (1, 3) é um ponto de f. Isto é, f(1) = 3. Disso obtemos a equação:

Ou seja,

.
Portanto, no final obtemos que:
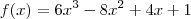 Observação
ObservaçãoEsse exercício pode tranquilamente ser proposto para uma pessoa que já estudou derivadas de polinômios. Não é necessário que ela já tenha estudado o conceito de integrais para resolvê-lo.
 no ponto (1,3) é
no ponto (1,3) é 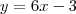

 é
é  e que a segunda derivada da função é
e que a segunda derivada da função é  . Não precisa resolver, só me dá uma luz de como utilizar essas informações por favor!
. Não precisa resolver, só me dá uma luz de como utilizar essas informações por favor!



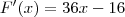 ?
?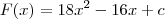 , sendo
, sendo 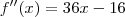 , temos que
, temos que  .
. . Mas, da informação 1) temos que essa reta é
. Mas, da informação 1) temos que essa reta é  .
.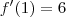 ficamos com a equação:
ficamos com a equação:
 . Isso significa que
. Isso significa que 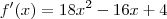 .
.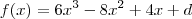 , sendo
, sendo 
 .
.