 por giulioaltoe » Qui Jul 21, 2011 17:04
por giulioaltoe » Qui Jul 21, 2011 17:04
eu tenho a expressão

pede pra eu achar a derivada!eu encontrei o valor

e no wolfram alpha ao inves de -3 ta dando +1, ja revisei a conta e nao estou achando meu erro!!
ve se alguem da um help ai...valew!
-
giulioaltoe
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Jun 23, 2011 21:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia metalurgica e mat - UENF
- Andamento: cursando
 por LuizAquino » Qui Jul 21, 2011 17:08
por LuizAquino » Qui Jul 21, 2011 17:08
Envie a sua resolução para que possamos identificar onde está o problema.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por giulioaltoe » Qui Jul 21, 2011 19:33
por giulioaltoe » Qui Jul 21, 2011 19:33

apos cortar os termos comuns.. desenvolvi a derivada
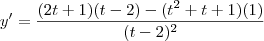
e isso gerou
![\frac{2t^2-4t+t-2-t^2-t-1}{(t-2)^2}[\tex] = [tex]\frac{t^2-4t-3}{(t-2)^2} \frac{2t^2-4t+t-2-t^2-t-1}{(t-2)^2}[\tex] = [tex]\frac{t^2-4t-3}{(t-2)^2}](/latexrender/pictures/4fb82039c4ee52c3e4d4c41f0e15e066.png)
... ai ???
-
giulioaltoe
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Jun 23, 2011 21:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia metalurgica e mat - UENF
- Andamento: cursando
 por MarceloFantini » Qui Jul 21, 2011 19:51
por MarceloFantini » Qui Jul 21, 2011 19:51
Esta é a resposta, não há mais simplificações possíveis.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por giulioaltoe » Qui Jul 21, 2011 19:57
por giulioaltoe » Qui Jul 21, 2011 19:57
uhum, mas quando joguei a conta no wolfram alpha nao bateu a resposta!
-
giulioaltoe
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Jun 23, 2011 21:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia metalurgica e mat - UENF
- Andamento: cursando
 por giulioaltoe » Qui Jul 21, 2011 20:16
por giulioaltoe » Qui Jul 21, 2011 20:16
hum e mesmo, sempre erro esses detalhezinhos... perdi quase 1 ponto numa prova que fiz so em erro assim!! vlw ai.. e isso msm!
-
giulioaltoe
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Jun 23, 2011 21:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia metalurgica e mat - UENF
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 12550 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
-
- [derivada] derivada pela definição da secante
por TheKyabu » Sáb Out 27, 2012 23:24
- 2 Respostas
- 10879 Exibições
- Última mensagem por TheKyabu

Dom Out 28, 2012 11:44
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Com duas variáveis e derivada mista
por leticiaeverson » Dom Abr 22, 2018 00:39
- 3 Respostas
- 13186 Exibições
- Última mensagem por Gebe

Dom Abr 22, 2018 17:11
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada]derivada de função de raiz cúbica
por armando » Sáb Jul 20, 2013 15:22
- 4 Respostas
- 14791 Exibições
- Última mensagem por armando

Dom Jul 21, 2013 22:17
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADA] DERIVADA POR DEFINIÇÃO DA RAIZ DO MÓDULO DE X
por Matheusgdp » Qua Set 16, 2015 04:07
- 2 Respostas
- 5106 Exibições
- Última mensagem por Matheusgdp

Qui Set 17, 2015 18:31
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 pede pra eu achar a derivada!eu encontrei o valor
pede pra eu achar a derivada!eu encontrei o valor  e no wolfram alpha ao inves de -3 ta dando +1, ja revisei a conta e nao estou achando meu erro!!
e no wolfram alpha ao inves de -3 ta dando +1, ja revisei a conta e nao estou achando meu erro!!
 pede pra eu achar a derivada!eu encontrei o valor
pede pra eu achar a derivada!eu encontrei o valor  e no wolfram alpha ao inves de -3 ta dando +1, ja revisei a conta e nao estou achando meu erro!!
e no wolfram alpha ao inves de -3 ta dando +1, ja revisei a conta e nao estou achando meu erro!!

 apos cortar os termos comuns.. desenvolvi a derivada
apos cortar os termos comuns.. desenvolvi a derivada 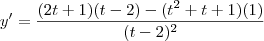 e isso gerou
e isso gerou ![\frac{2t^2-4t+t-2-t^2-t-1}{(t-2)^2}[\tex] = [tex]\frac{t^2-4t-3}{(t-2)^2} \frac{2t^2-4t+t-2-t^2-t-1}{(t-2)^2}[\tex] = [tex]\frac{t^2-4t-3}{(t-2)^2}](/latexrender/pictures/4fb82039c4ee52c3e4d4c41f0e15e066.png) ... ai ???
... ai ???







