 por Neperiano » Qua Jun 22, 2011 09:54
por Neperiano » Qua Jun 22, 2011 09:54
Ola
I don't know if you talk english, because you put in english, but will go to speak portuguese, i f you are english or american, talk-me, i put in your language.
Primeiro corte a integral dara 1 + tg^nx , dai calcule ela e aproxime b de Pi/2 e a 0, axo q eh isso
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Desigualdade!
por Questioner » Dom Mai 16, 2010 17:13
- 1 Respostas
- 1662 Exibições
- Última mensagem por Douglasm

Dom Mai 16, 2010 18:37
Sistemas de Equações
-
- Desigualdade
por Claudin » Qui Jan 17, 2013 14:50
- 2 Respostas
- 2562 Exibições
- Última mensagem por Claudin

Sex Jan 18, 2013 20:14
Álgebra Linear
-
- Resolvendo a desigualdade...
 por Aliocha Karamazov » Qua Abr 06, 2011 19:55
por Aliocha Karamazov » Qua Abr 06, 2011 19:55
- 3 Respostas
- 2583 Exibições
- Última mensagem por Aliocha Karamazov

Qua Abr 06, 2011 23:20
Funções
-
- Desigualdade Triangular
por Claudin » Sex Set 09, 2011 09:40
- 1 Respostas
- 1875 Exibições
- Última mensagem por LuizAquino

Sex Set 09, 2011 10:56
Cálculo: Limites, Derivadas e Integrais
-
- desigualdade:prova
por Victor Gabriel » Ter Jun 18, 2013 13:48
- 0 Respostas
- 1104 Exibições
- Última mensagem por Victor Gabriel

Ter Jun 18, 2013 13:48
Teoria dos Números
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
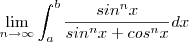





 .
.
 :
: