Como calcular derivadas com a constante "e"

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

Como calcular derivadas com a constante "e"

Regras do fórum
Responder

Como calcular derivadas com a constante "e"

Mensagempor fer_carnie » Seg Jun 20, 2011 20:40

Eu não sei como calcular derivadas com a constante "e", por favor vcs podem me explicar como eu faço para calcular?
Envio um exercício que tem a constante, talvez vcs possam usá-lo para me explicar.
A)Ache a taxa de variação do preço por frasco quando x=1000 e x=2000.
p=100{e}^{-0,0002x}+150
onde, p= preço de varejo/unidade e x=quantidade de frascos demandada.
B) qual é o preço do frasco quando x=1000 e x=2000?
fer_carnie
Novo Usuário
Novo Usuário
 
Mensagens: 1
Registrado em: Seg Jun 20, 2011 20:28
Formação Escolar: GRADUAÇÃO
Área/Curso: Administração
Andamento: cursando
Voltar ao topo

Re: Como calcular derivadas com a constante "e"

Mensagempor Fabio Cabral » Seg Jun 20, 2011 22:22

Boa noite.

A regra de Derivação para Função Exponencial (base e) é: f(x)={e}^{g(x)}\rightarrow f'(x)= g'(x).{e}^{g(x)}

Exemplo:
f(x)={e}^{2x}

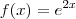
Aplicando a regra acima:

f'(x)=2.{e}^{2x}
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
Fabio Cabral
Colaborador Voluntário
Colaborador Voluntário
 
Mensagens: 122
Registrado em: Qua Out 06, 2010 11:33
Localização: Brasília-DF
Formação Escolar: GRADUAÇÃO
Área/Curso: Ciência da computação
Andamento: cursando
Voltar ao topo
Responder

Voltar para Cálculo: Limites, Derivadas e Integrais

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes

 


Tópico Popular

Assunto: Taxa de variação
Autor: felipe_ad - Ter Jun 29, 2010 19:44

Como resolvo uma questao desse tipo:

Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?

A letra (a) consegui resolver e cheguei no resultado correto de \frac{4\pi{r}^{2}}{3}
Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é 1,066\pi

Alguem me ajuda? Agradeço desde já.

Assunto: Taxa de variação
Autor: Elcioschin - Qua Jun 30, 2010 20:47

V = (1/3)*pi*r²*h ----> h = 4r/3

V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³

Derivando:

dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3

Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s

Assunto: Taxa de variação
Autor: Guill - Ter Fev 21, 2012 21:17

Temos que o volume é dado por:

V = \frac{4\pi}{3}r^2


Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

\frac{dV}{dt} = \frac{8\pi.r}{3}.\frac{dr}{dt}


Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:

\frac{dV}{dt} = \frac{8\pi.2}{3}.\frac{2}{10}

\frac{dV}{dt} = \frac{16\pi}{15}

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

Índice do fórum