 por paula luna » Ter Jun 07, 2011 15:15
por paula luna » Ter Jun 07, 2011 15:15
Oi!
Meu professor fez essa derivada no quadro mas nao intendi nada... alguem pode me explicar?!

Tipo ele fez por regra da cadeia mas primeiro ele pôs a funçao com exponencial assim:
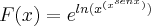
eu sei que essa funçao e^ln ... é a mesma coisa que a funçao la em cima, no entanto nao intendo no que isso ajuda pra fazer a questao e consequentemente isso confundiu todo resto da questao. Tentei fazer normal por regra da cadeia mas o resultado fico algo estranho e longe da resposta que ele (professor) chegou. Desculpe os varios erros de gramatica... tava com pressa xD.

pra quem leu !! e


pra quem leu e respondeu

-
paula luna
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Qui Mai 05, 2011 21:56
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Ter Jun 07, 2011 18:26
por LuizAquino » Ter Jun 07, 2011 18:26
Considere que
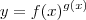
, com
f(
x) > 0.
Lembrando-se das propriedades de logaritmos, sabemos que
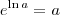
e que

.
Desse modo, temos que
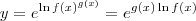
.
Considerando que
f e
g são diferenciáveis em um mesmo domínio, derivando ambos os membros dessa equação temos que:
![y^\prime = \left[e^{g(x)\ln f(x)}\right]^\prime = \left[g(x)\ln f(x)\right]^\prime e^{g(x)\ln f(x)} = \left[g(x)\ln f(x)\right]^\prime f(x)^{g(x)}} y^\prime = \left[e^{g(x)\ln f(x)}\right]^\prime = \left[g(x)\ln f(x)\right]^\prime e^{g(x)\ln f(x)} = \left[g(x)\ln f(x)\right]^\prime f(x)^{g(x)}}](/latexrender/pictures/98377d88eb36f89e1241ecf0f67bfc7f.png)
. (Lembrete: pela Regra da Cadeia, temos que
![[e^u]^\prime = u^\prime e^u [e^u]^\prime = u^\prime e^u](/latexrender/pictures/df80f23670eae9f57797b16b8f0a96ec.png)
.)
Desse modo, temos uma regra geral para esses casos:
![\left[f(x)^{g(x)}\right]^\prime = \left[g(x)\ln f(x)\right]^\prime f(x)^{g(x)} \left[f(x)^{g(x)}\right]^\prime = \left[g(x)\ln f(x)\right]^\prime f(x)^{g(x)}](/latexrender/pictures/ce83c48ba6bea3871cc8d7c3ee01c8f0.png)
.
No exercício, temos

. Fazendo

e

temos que
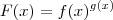
. Agora basta aplicar a regra acima.
Note que será necessário derivar a função
g. Fazendo
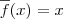
e
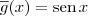
temos que
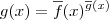
. Daí basta aplicar a regra novamente para essa função.
paula luna escreveu:Desculpe os varios erros de gramatica... tava com pressa xD.
Procure ter mais cuidado da próxima vez. É ruim ler algo como "
intender".

-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por paula luna » Ter Jun 07, 2011 21:21
por paula luna » Ter Jun 07, 2011 21:21
Ok, otimo! consegui fazer facilmente a questao seguindo os passos, porem continuo com 2 duvidas:
1ª) quando é dito "...temos uma regra geral para esses casos..." , que casos sao estes?
2ª) Por que nao pode ser feito a regra da cadeia tomando o expoente x^senx como um 'u' e fazendo x^u ?
Eu realmente nao vejo o porquê de usar toda aquela historia de logaritmo natural e funçao expoencial para simplificar a funçao inicial ao inves de aplicar a regra da cadeia direto.
Desculpa eu incomoda tanto com essas questoes mas meu professor realmente nao sabe explicar o que ele faz no quadro e os monitores menos ainda.
-
paula luna
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Qui Mai 05, 2011 21:56
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Ter Jun 07, 2011 22:46
por LuizAquino » Ter Jun 07, 2011 22:46
paula luna escreveu:1ª) quando é dito "...temos uma regra geral para esses casos..." , que casos sao estes?
Leia com mais atenção a minha mensagem.
Considere que 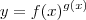 , com f(x) > 0. (...)Considerando que f e g são diferenciáveis em um mesmo domínio (...)(...) temos uma regra geral para esses casos:
, com f(x) > 0. (...)Considerando que f e g são diferenciáveis em um mesmo domínio (...)(...) temos uma regra geral para esses casos: ![\left[f(x)^{g(x)}\right]^\prime = \left[g(x)\ln f(x)\right]^\prime f(x)^{g(x)} \left[f(x)^{g(x)}\right]^\prime = \left[g(x)\ln f(x)\right]^\prime f(x)^{g(x)}](/latexrender/pictures/ce83c48ba6bea3871cc8d7c3ee01c8f0.png) .
.paula luna escreveu:2ª) Por que nao pode ser feito a regra da cadeia tomando o expoente x^senx como um 'u' e fazendo x^u ?
Para aplicar a regra da cadeia devemos ter uma função composta. Ou seja, devemos ter algo do tipo f(u(x)).
Agora, reflita sobre a seguinte questão: se colocarmos

e
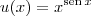
é verdadeiro que
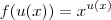
?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por paula luna » Sex Jun 10, 2011 04:48
por paula luna » Sex Jun 10, 2011 04:48
-
paula luna
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Qui Mai 05, 2011 21:56
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- senx
por camilaarbar » Qua Mai 13, 2009 21:57
- 3 Respostas
- 1971 Exibições
- Última mensagem por Cleyson007

Sáb Mai 16, 2009 15:24
Trigonometria
-
- [integral] senx cos^2x dx
por ericamila2 » Sáb Out 15, 2011 18:15
- 1 Respostas
- 3783 Exibições
- Última mensagem por LuizAquino

Sáb Out 15, 2011 19:06
Cálculo: Limites, Derivadas e Integrais
-
- a primitiva senx dx
por Ana Maria da Silva » Sex Nov 29, 2013 08:52
- 2 Respostas
- 1389 Exibições
- Última mensagem por Ana Maria da Silva

Sáb Nov 30, 2013 08:20
Cálculo: Limites, Derivadas e Integrais
-
- o domínio da função z=f(x,y)=(x?y)/(senx?seny)
por eduardo_ochoa » Sex Set 08, 2017 17:13
- 0 Respostas
- 2590 Exibições
- Última mensagem por eduardo_ochoa

Sex Set 08, 2017 17:13
Funções
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 12554 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

 pra quem leu !! e
pra quem leu !! e 
 pra quem leu e respondeu
pra quem leu e respondeu 


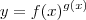 , com
, com 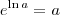 e que
e que  .
.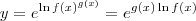 .
.![y^\prime = \left[e^{g(x)\ln f(x)}\right]^\prime = \left[g(x)\ln f(x)\right]^\prime e^{g(x)\ln f(x)} = \left[g(x)\ln f(x)\right]^\prime f(x)^{g(x)}} y^\prime = \left[e^{g(x)\ln f(x)}\right]^\prime = \left[g(x)\ln f(x)\right]^\prime e^{g(x)\ln f(x)} = \left[g(x)\ln f(x)\right]^\prime f(x)^{g(x)}}](/latexrender/pictures/98377d88eb36f89e1241ecf0f67bfc7f.png) . (Lembrete: pela Regra da Cadeia, temos que
. (Lembrete: pela Regra da Cadeia, temos que ![[e^u]^\prime = u^\prime e^u [e^u]^\prime = u^\prime e^u](/latexrender/pictures/df80f23670eae9f57797b16b8f0a96ec.png) .)
.)![\left[f(x)^{g(x)}\right]^\prime = \left[g(x)\ln f(x)\right]^\prime f(x)^{g(x)} \left[f(x)^{g(x)}\right]^\prime = \left[g(x)\ln f(x)\right]^\prime f(x)^{g(x)}](/latexrender/pictures/ce83c48ba6bea3871cc8d7c3ee01c8f0.png) .
. . Fazendo
. Fazendo  e
e  temos que
temos que 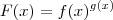 . Agora basta aplicar a regra acima.
. Agora basta aplicar a regra acima.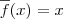 e
e 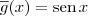 temos que
temos que 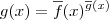 . Daí basta aplicar a regra novamente para essa função.
. Daí basta aplicar a regra novamente para essa função.

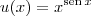 é verdadeiro que
é verdadeiro que 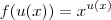 ?
?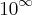 , vlw pela ajuda msm.
, vlw pela ajuda msm. .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.