Vamos supor que você tenha uma função do tipo
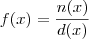
, sendo que
n(x) e
d(x) são funções contínuas.
A função
f apenas será descontínua em algum valor
x se
d(x) = 0.
No seu exercício, a função será descontínua caso

.
Uma assíntota vertical ao gráfico de
f ocorre quando pelo menos um dos limites abaixo for verdadeiro:
(i)
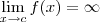
(ii)
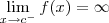
(iii)
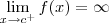
Nesse caso, dizemos que a equação da assíntota vertical é dada por x = c.
No seu exercício, basta analisar se há algum ponto c para o qual um dos limites acima acontece. Aqui fica uma dica: se
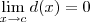
, então a função
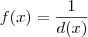
tem uma assíntota vertical dada por x = c.
Por outro lado, uma assíntota horizontal ao gráfico de
f ocorre quando pelo menos um dos limites abaixo for verdadeiro:
(i)
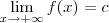
(ii)
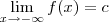
Nesse caso, dizemos que a equação da assíntota horizontal é dada por y = c.
No seu exercício, basta você calcular o limite
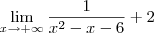
. Para isso, aqui vai outra dica: divida tanto o numerador quanto o denominador da fração por

. Em seguida, lembre-se que
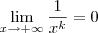
(com
k natural não nulo).
Por fim, dizemos que um limite não existe quando os seus limites laterais são distintos. Isto é, o limite
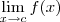
não existe caso
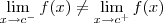
.
SugestãoEu gostaria de recomendar que você assista as vídeo-aulas "04. Cálculo I - Limites e Continuidade", "05. Cálculo I - Limites Infinitos" e "06. Cálculo I - Limites no Infinito". Elas estão disponíveis em meu canal:
http://www.youtube.com/LCMAquino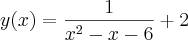


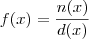 , sendo que
, sendo que  .
.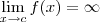
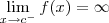
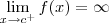
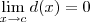 , então a função
, então a função 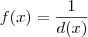 tem uma assíntota vertical dada por x = c.
tem uma assíntota vertical dada por x = c.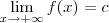
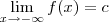
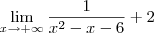 . Para isso, aqui vai outra dica: divida tanto o numerador quanto o denominador da fração por
. Para isso, aqui vai outra dica: divida tanto o numerador quanto o denominador da fração por  . Em seguida, lembre-se que
. Em seguida, lembre-se que 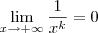 (com
(com 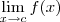 não existe caso
não existe caso 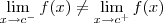 .
.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.