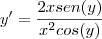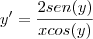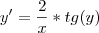por Maykids » Seg Mai 23, 2011 18:25
por Maykids » Seg Mai 23, 2011 18:25
por favor vejam o que eu estou fazendo de errado nessa conta.
f(x) = xy
estou usando a regra do produto:
f'(x) = (1.y)+ (1.y')*x
f'(x) = y+y'x
y'=y/x
so que o resultado não é esse, pelo menos no wolframalpha.com
la da apenas, Y
obrigado
att,
-
Maykids
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Dom Mar 20, 2011 12:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de computação
- Andamento: cursando
 por LuizAquino » Seg Mai 23, 2011 18:31
por LuizAquino » Seg Mai 23, 2011 18:31
Vamos considerar que y é uma função de x (isto é, y = f(x)) e queremos derivar y = xy.
Temos que:
(y)' = (xy)'
y' = (x)'y + x(y)'
y' = y + xy'
y' = y/(1-x)
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Maykids » Seg Mai 23, 2011 18:51
por Maykids » Seg Mai 23, 2011 18:51
y' = y/(1-x)
não entendi o que aconteceu nesse passo.
antes tinham dois y', agora passou a ficar so com 1.
-
Maykids
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Dom Mar 20, 2011 12:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de computação
- Andamento: cursando
 por LuizAquino » Seg Mai 23, 2011 18:56
por LuizAquino » Seg Mai 23, 2011 18:56
Note que y' = y + xy' é o mesmo que y' - xy' = y.
O que acontece se colocarmos y' em fator comum no primeiro membro?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Maykids » Seg Mai 23, 2011 18:59
por Maykids » Seg Mai 23, 2011 18:59
Cara eu pensei na evidencia so que axei que estava errado, rss, muito obrigado aquino, suas aulas no youtube tambem são otimas, hahaha.
-
Maykids
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Dom Mar 20, 2011 12:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de computação
- Andamento: cursando
 por Maykids » Seg Mai 23, 2011 19:56
por Maykids » Seg Mai 23, 2011 19:56
por favor veja se eu fiz certo esse exercicio:
y'=x²sen(y)
y'= 2xsen(y) + x²cos(y)y'
y'cos(y)x²= 2xsen(y)
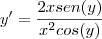
=
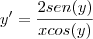
ainda:
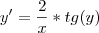
-
Maykids
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Dom Mar 20, 2011 12:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de computação
- Andamento: cursando
 por LuizAquino » Seg Mai 23, 2011 22:23
por LuizAquino » Seg Mai 23, 2011 22:23
Do segundo para o terceiro passo está errado.
Você não colocou o termo y' em evidência de maneira correta.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Maykids » Ter Mai 24, 2011 03:14
por Maykids » Ter Mai 24, 2011 03:14
"ora" acho que esqueci do sinal de menos.
a) y = x²sen(y)
y'cos(y)x² = - 2xsen(y)
y'= -2xsen(y)/x²cos(y)
y'= -2sen(y)/xcos(y)
-
Maykids
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Dom Mar 20, 2011 12:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de computação
- Andamento: cursando
 por LuizAquino » Ter Mai 24, 2011 14:52
por LuizAquino » Ter Mai 24, 2011 14:52
Você continua errando.
y' = 2xsen(y) + x²cos(y)y'
y' - x²cos(y)y' = 2xsen(y)
y'[1 - x²cos(y)] = 2xsen(y)
y' = [2xsen(y)]/[1 - x²cos(y)]
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Maykids » Ter Mai 24, 2011 15:26
por Maykids » Ter Mai 24, 2011 15:26
hmmm..é porque eu n sabia que o y q representa a funcao continua na conta eu achei qe ele desaparecia =)
obrigado de novo
-
Maykids
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Dom Mar 20, 2011 12:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada Parcial - Teorema das Funções Implícitas]
por raimundoocjr » Qua Nov 06, 2013 21:16
- 0 Respostas
- 1184 Exibições
- Última mensagem por raimundoocjr

Qua Nov 06, 2013 21:16
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Dificuldade para calcular derivadas CDI 1
por srmai » Seg Nov 04, 2013 01:21
- 0 Respostas
- 2262 Exibições
- Última mensagem por srmai

Seg Nov 04, 2013 01:21
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Interpretação de derivadas e funções
por vinik1 » Qua Out 12, 2011 16:03
- 5 Respostas
- 7474 Exibições
- Última mensagem por vinik1

Qui Out 13, 2011 10:48
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Derivadas em pontos dados
por MarlonMO250 » Sex Mar 01, 2013 21:02
- 6 Respostas
- 4944 Exibições
- Última mensagem por Russman

Sáb Mar 02, 2013 03:42
Cálculo: Limites, Derivadas e Integrais
-
- (derivadas) derivadas com raiz como se faz
por jana garcia » Qua Jun 25, 2014 00:28
- 1 Respostas
- 2965 Exibições
- Última mensagem por e8group

Qua Jun 25, 2014 01:13
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.