 por romulo39 » Dom Abr 03, 2011 20:58
por romulo39 » Dom Abr 03, 2011 20:58
Boa noite
Favor tirar uma duvida, na verdade quero saber os principio para integrar, gosto de tirar minhas duvidas com exemplos como o que envio abaixo , por parte.
desde ja agradeço
Verifique se a funçao dada é uma soluçao diferencial ( c1.e c2 sao constantes)
romulo netto
2xy dx +(x²+2Y)dy = 0; x²y + y² = C1
-
romulo39
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Mar 31, 2011 23:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: CURSO TECNICO EM LICENCIATURA MATEMATICA
- Andamento: cursando
 por LuizAquino » Seg Abr 04, 2011 14:39
por LuizAquino » Seg Abr 04, 2011 14:39
Note que a equação diferencial
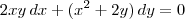
é a mesma que

.
Vamos agora derivar a função (implícita, y=f(x)) dada por

.
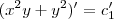


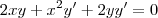


Lembrando que fizemos y como uma função de x, temos que a notação
y' e a notação

são equivalente, portanto:

Agora, uma curiosidade: Como funciona um Curso Técnico em Licenciatura Matemática? Isto é, qual é a grade curricular? Qual é a duração? Você poderia, por favor, indicar a página da instituição que oferece tal curso para que eu possa ler mais a respeito?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação Diferencial.
por Higor » Seg Fev 21, 2011 13:12
- 4 Respostas
- 12212 Exibições
- Última mensagem por Higor

Seg Fev 21, 2011 14:46
Cálculo: Limites, Derivadas e Integrais
-
- Equação diferencial
por jacquelline » Qui Mai 17, 2012 11:04
- 2 Respostas
- 2074 Exibições
- Última mensagem por jacquelline

Sáb Mai 19, 2012 20:37
Cálculo: Limites, Derivadas e Integrais
-
- Equação diferencial - 1
por Cleyson007 » Qua Nov 07, 2012 21:09
- 8 Respostas
- 3852 Exibições
- Última mensagem por MarceloFantini

Qui Nov 08, 2012 17:05
Cálculo: Limites, Derivadas e Integrais
-
- Equação diferencial - 2
por Cleyson007 » Qua Nov 07, 2012 21:14
- 1 Respostas
- 1484 Exibições
- Última mensagem por e8group

Qua Nov 14, 2012 10:06
Cálculo: Limites, Derivadas e Integrais
-
- Equação diferencial - 3
por Cleyson007 » Qua Nov 07, 2012 21:19
- 1 Respostas
- 1367 Exibições
- Última mensagem por young_jedi

Qui Nov 08, 2012 12:33
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


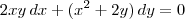 é a mesma que
é a mesma que  .
. .
.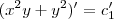


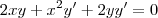


 são equivalente, portanto:
são equivalente, portanto:
