![f(x)= \lim_{n\rightarrow\propto} \frac{{x}^{n+2}}{\sqrt[2]{{2}^{2n}+{x}^{2n}}} f(x)= \lim_{n\rightarrow\propto} \frac{{x}^{n+2}}{\sqrt[2]{{2}^{2n}+{x}^{2n}}}](/latexrender/pictures/5dd794082eb22cf894a100dc9fade06f.png) ; x > 0
; x > 0gente, alguém me da uma luz de como eu começo a fazer isso?? não tenho a mínima ideia de como começar

![f(x)= \lim_{n\rightarrow\propto} \frac{{x}^{n+2}}{\sqrt[2]{{2}^{2n}+{x}^{2n}}} f(x)= \lim_{n\rightarrow\propto} \frac{{x}^{n+2}}{\sqrt[2]{{2}^{2n}+{x}^{2n}}}](/latexrender/pictures/5dd794082eb22cf894a100dc9fade06f.png) ; x > 0
; x > 0

 (o que poderemos fazer já que x>0).
(o que poderemos fazer já que x>0).
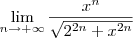 para cada um dos casos descritos anteriormente.
para cada um dos casos descritos anteriormente.



Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes

 .
.
 :
: