 por MarcusPassos » Qui Mar 03, 2011 17:37
por MarcusPassos » Qui Mar 03, 2011 17:37
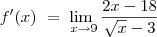
Gostaria de pedir a ajudar de vocês para responder esta questão , eu multiplico e divido pelo conjugado , mas não acho o resultado correto.
Grato desde ja!
-
MarcusPassos
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Mar 03, 2011 17:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. mecatronica
- Andamento: cursando
 por LuizAquino » Qui Mar 03, 2011 18:40
por LuizAquino » Qui Mar 03, 2011 18:40
MarcusPassos escreveu:eu multiplico e divido pelo conjugado , mas não acho o resultado correto.
Poste aqui o que você fez. Desse modo, podemos achar onde está o erro.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por MarcusPassos » Qui Mar 03, 2011 19:06
por MarcusPassos » Qui Mar 03, 2011 19:06
eu paro nisso , porq nao da certo ->
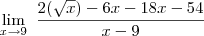
-
MarcusPassos
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Mar 03, 2011 17:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. mecatronica
- Andamento: cursando
 por MarcusPassos » Qui Mar 03, 2011 21:22
por MarcusPassos » Qui Mar 03, 2011 21:22
Muito , Muito obrigado mesmo amigo ,ja tava arrancando os poucos fios de kbelo que tenho

-
MarcusPassos
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Mar 03, 2011 17:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. mecatronica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limites] indeterminação?
por rafaelbr91 » Ter Mar 27, 2012 18:48
- 3 Respostas
- 2098 Exibições
- Última mensagem por nietzsche

Ter Mar 27, 2012 19:31
Cálculo: Limites, Derivadas e Integrais
-
- Indeterminação de Limites
por dsidney30 » Sex Mai 03, 2013 15:53
- 1 Respostas
- 1474 Exibições
- Última mensagem por young_jedi

Dom Mai 05, 2013 19:07
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] - Indeterminação e Impossibilidade
por Scheu » Qui Fev 02, 2012 00:14
- 2 Respostas
- 3840 Exibições
- Última mensagem por Scheu

Sex Fev 03, 2012 00:03
Cálculo: Limites, Derivadas e Integrais
-
- Indeterminação limites fundamental
por Rosi7 » Sex Mai 22, 2015 11:49
- 3 Respostas
- 4626 Exibições
- Última mensagem por Jennicop

Ter Dez 22, 2015 03:20
Cálculo: Limites, Derivadas e Integrais
-
- Limites - Indeterminação do tipo 0X+infinito
por Pollyanna Moraes » Sáb Abr 28, 2012 15:04
- 1 Respostas
- 2865 Exibições
- Última mensagem por Guill

Dom Abr 29, 2012 09:05
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
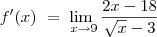

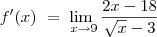


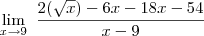

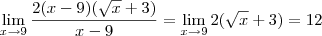





 .
.



