 por Kelvin Brayan » Dom Fev 20, 2011 17:04
por Kelvin Brayan » Dom Fev 20, 2011 17:04
Olá, será que alguém poderia me ajudar com a seguinte questão de matemática?
01.(UFU-MG) um maratonista calcula que, se correr a uma velocidade constante de 10km/h, chegará ao fim do percuso às 10:00 horas. Contudo, se sua velocidade constante for 15 km/h, ele chegará às 08:00 horas. Para que ele chegue exatamente às 09:00 horas, sua velocidade constante deverá ser de...
Tentei resolvê-la, mas não consegui. Nem ao menos tenho ideia de como iniciá-la !
-
Kelvin Brayan
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Dom Fev 20, 2011 16:50
- Localização: Varginha - MG
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Inglês
- Andamento: cursando
 por Molina » Seg Fev 21, 2011 02:01
por Molina » Seg Fev 21, 2011 02:01
Boa noite, Kelvin.
Primeiramente temos que saber que
velocidade é deslocamento sobre tempo:
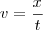
Agora, pelos dados do exercício temos que:

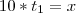
e


Perceba que x (distância) é a mesma nas duas equações e que a diferença entre os tempos t de uma para a outra é de 2h. Então podemos fazer:

E com isso:
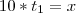
e

Igualando as duas equações:

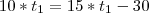

Este era o tempo que ele demoraria chegando as 10:00. Por isso, podemos concluir que a corrida começará as 4:00.
Pela fórmula da velocidade você pode concluir que a distância x percorrida neste corrida é de 60km.
Agora fica fácil usar novamente a fórmula da velocidade para descobrir a velocidade para chegar as 9:00.

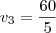
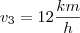
Qualquer dúvida, informe.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Kelvin Brayan » Qua Fev 23, 2011 09:50
por Kelvin Brayan » Qua Fev 23, 2011 09:50
Muito obrigado, a resposta está corretíssima.
Valeu mesmo aí pela força !
-
Kelvin Brayan
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Dom Fev 20, 2011 16:50
- Localização: Varginha - MG
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Inglês
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão matemática
por gustavomatteo » Qui Mar 02, 2017 18:45
- 0 Respostas
- 2602 Exibições
- Última mensagem por gustavomatteo

Qui Mar 02, 2017 18:45
Lógica e Conjuntos
-
- Questão de matemática e administração
por 1marcus » Sáb Nov 03, 2018 23:48
- 0 Respostas
- 4578 Exibições
- Última mensagem por 1marcus

Sáb Nov 03, 2018 23:48
Matemática Financeira
-
- [questao do cefet mg matemática]
por tayna01 » Ter Abr 22, 2014 12:13
- 1 Respostas
- 2712 Exibições
- Última mensagem por adauto martins

Seg Jan 05, 2015 14:52
Números Complexos
-
- QUESTÃO DE MATEMÁTICA FINANCEIRA COM LOGARÍTIMOS
por saulfiterman » Seg Ago 20, 2012 21:26
- 1 Respostas
- 3480 Exibições
- Última mensagem por LuizAquino

Seg Set 24, 2012 10:50
Logaritmos
-
- Matemática Financeira - Questão com Porcentagem
por joedsonazevedo » Qui Nov 08, 2012 14:50
- 6 Respostas
- 6746 Exibições
- Última mensagem por saberdigitalnet

Sáb Nov 24, 2012 21:01
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


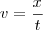

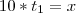





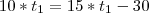


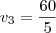
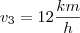


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
